Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Botelho, Fernanda
Jamison, James
and
Molnár, Lajos
2013.
Algebraic reflexivity of isometry groups and automorphism groups of some operator structures.
Journal of Mathematical Analysis and Applications,
Vol. 408,
Issue. 1,
p.
177.
Hosseini, Maliheh
2017.
Generalized 2-local isometries of spaces of continuously differentiable functions.
Quaestiones Mathematicae,
Vol. 40,
Issue. 8,
p.
1003.
Jiménez-Vargas, Antonio
Li, Lei
Peralta, Antonio M.
Wang, Liguang
and
Wang, Ya-Shu
2018.
2-Local standard isometries on vector-valued Lipschitz function spaces.
Journal of Mathematical Analysis and Applications,
Vol. 461,
Issue. 2,
p.
1287.
Molnár, Lajos
2019.
On 2-local *-automorphisms and 2-local isometries of B(H).
Journal of Mathematical Analysis and Applications,
Vol. 479,
Issue. 1,
p.
569.
Cabrera-Padilla, M. G.
Jiménez-Vargas, A.
and
Villegas-Vallecillos, Moisés
2020.
Associative and Non-Associative Algebras and Applications.
Vol. 311,
Issue. ,
p.
51.
Alimohammadi, Davood
and
Pazandeh, Hadis
2020.
2-Local isometries between Banach algebras of continuous functions with involution.
Banach Journal of Mathematical Analysis,
Vol. 14,
Issue. 1,
p.
203.
Jiménez-Vargas, A.
and
Villegas-Vallecillos, Moisés
2020.
2-Iso-reflexivity of pointed Lipschitz spaces.
Journal of Mathematical Analysis and Applications,
Vol. 491,
Issue. 2,
p.
124359.
Alimohammadi, Davood
and
Bagheri, Reyhaneh
2020.
2-Local uniform isometries between complex Lipschitz algebras.
Annals of Functional Analysis,
Vol. 11,
Issue. 2,
p.
406.
Hosseini, Maliheh
2020.
2-Local isometries between spaces of functions of bounded variation.
Positivity,
Vol. 24,
Issue. 4,
p.
1101.
Jiménez-Vargas, A.
and
Sady, Fereshteh
2021.
On 2-local diameter-preserving maps between C(X)-spaces.
Positivity,
Vol. 25,
Issue. 3,
p.
867.
Jiménez-Vargas, Antonio
and
Ramírez, María Isabel
2021.
Algebraic Reflexivity of Non-Canonical Isometries on Lipschitz Spaces.
Mathematics,
Vol. 9,
Issue. 14,
p.
1635.
OI, SHIHO
2021.
A SPHERICAL VERSION OF THE KOWALSKI–SŁODKOWSKI THEOREM AND ITS APPLICATIONS.
Journal of the Australian Mathematical Society,
Vol. 111,
Issue. 3,
p.
386.
Hosseini, Maliheh
2022.
2-Topological reflexivity of sets of isometries between bounded variation function spaces.
Positivity,
Vol. 26,
Issue. 2,
Koshimizu, Hironao
and
Miura, Takeshi
2022.
2-local real-linear isometries on C(1)([0, 1]).
Quaestiones Mathematicae,
Vol. 45,
Issue. 9,
p.
1353.
Miao, Feifei
Wang, Xiao
Li, Lei
and
Wang, Liguang
2022.
Two-local isometries on vector-valued differentiable functions.
Linear and Multilinear Algebra,
Vol. 70,
Issue. 13,
p.
2505.
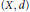 $(X,\,d)$ be a metric space, and let
$(X,\,d)$ be a metric space, and let 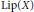 $\text{Lip(}X\text{)}$ denote the Banach space of all scalar-valued bounded Lipschitz functions
$\text{Lip(}X\text{)}$ denote the Banach space of all scalar-valued bounded Lipschitz functions 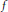 $f$ on
$f$ on 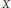 $X$ endowed with one of the natural norms
$X$ endowed with one of the natural norms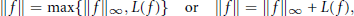 $$\left\| f \right\|\,=\,\max \{{{\left\| f \right\|}_{\infty }},\,L(f)\}\,\,\text{or}\,\,\left\| f \right\|\,=\,{{\left\| f \right\|}_{\infty }}\,+\,L(f),$$
$$\left\| f \right\|\,=\,\max \{{{\left\| f \right\|}_{\infty }},\,L(f)\}\,\,\text{or}\,\,\left\| f \right\|\,=\,{{\left\| f \right\|}_{\infty }}\,+\,L(f),$$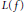 $L(f)$ is the Lipschitz constant of
$L(f)$ is the Lipschitz constant of 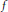 $f$. It is said that the isometry group of
$f$. It is said that the isometry group of 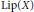 $\text{Lip(}X\text{)}$ is canonical if every surjective linear isometry of
$\text{Lip(}X\text{)}$ is canonical if every surjective linear isometry of 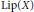 $\text{Lip(}X\text{)}$ is induced by a surjective isometry of
$\text{Lip(}X\text{)}$ is induced by a surjective isometry of 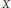 $X$. In this paper we prove that if
$X$. In this paper we prove that if 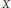 $X$ is bounded separable and the isometry group of
$X$ is bounded separable and the isometry group of 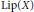 $\text{Lip(}X\text{)}$ is canonical, then every 2-local isometry of
$\text{Lip(}X\text{)}$ is canonical, then every 2-local isometry of 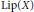 $\text{Lip(}X\text{)}$ is a surjective linear isometry. Furthermore, we give a complete description of all 2-local isometries of
$\text{Lip(}X\text{)}$ is a surjective linear isometry. Furthermore, we give a complete description of all 2-local isometries of 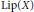 $\text{Lip(}X\text{)}$ when
$\text{Lip(}X\text{)}$ when 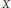 $X$ is bounded.
$X$ is bounded.