Article contents
Some Remarks on Indiscernibility1
Published online by Cambridge University Press: 01 January 2020
Extract
If α and α’ are distinct variables and ϕ and ϕ’ are open sentences of some language, where ϕ’ is the result of replacing one or more free occurrences of a in α with free occurrences of α’ in ϕ’, then a universal closure of ⌜(α=α’ → (ϕ → ϕ’))⌝, is an indiscernibility principle of that language. For instance, (1) is an indiscernibility principle.
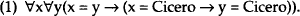
The existence of opaque constructions falsifies the familiar unrestricted principle of substitution which affirms that co-referential expressions are intersubstitutable in all contexts without change of truth-value. But indiscernibility principles are another matter. Not every counter-example to the unrestricted principle of substitution is a counter-example to some indiscernibility principle. Indeed, it is likely to be thought that there is no counter-example to any indiscernibility principle, and that the semantics of variables and objectual quantification ensures that all indiscernibility principles are true.
- Type
- Research Article
- Information
- Canadian Journal of Philosophy Supplementary Volume , Volume 18: Return of the a priori , 1992 , pp. 167 - 178
- Copyright
- Copyright © The Authors 1992
Footnotes
Earlier versions of this paper were read at the Alberta Philosophy Conference at Banff, 1987 and at the Ninth International Congress of Logic, Methodology, and Philosophy of Science at Uppsala, 1991.
References
2 Quine, W.V.Word and Object (Cambridge, MA: The MIT Press 1960), 167-8Google Scholar
3 Kaplan, David ‘Opacity’ in Hahn, L.E. and Schilpp, P.A. eds., The Philosophy of W.V. Quine (La Salle, IL: Open Court 1986), 274-5Google Scholar
4 Cartwright, Richard ‘Indiscemibility Principles’ in his Philosophical Essays (Cambridge, MA: The MIT Press 1987), 200-15Google Scholar
5 Richard, Mark also defends this view in his ‘Quantification and Leibniz’s Law,’ Philosophical Review 96 555-78, and in his Propositional Attitudes (Cambridge: Cambridge University Press 1990), 199-208.Google Scholar
6 Kaplan, 274-5. I have modified the notation to conform with the style of this essay.
7 Cartwright, 212-13. I have modified the notation to conform with the style of this essay.
8 Lewis, David ‘Counterpart Theory and Quantified Modal Logic’ in his Philosophical Papers Vol. 1 (Oxford: Oxford University Press 1983), 26-46Google Scholar
9 Kripke, SaulNaming and Necessity (Cambridge, MA: Harvard University Press 1980), 45Google Scholar
10 Because DL gives rise to false indiscernibility principles, it seems implausible that it defines a notion of metaphysical necessity. According to DL, (i) and (ii) are translated as (i)’ and (ii)’ respectively.
(i) λx[□x = x]a.
(ii) λx[∀w ∀b((Ww & lbw & Cbx) → b = b)a.
(iii) λxλy[□ = y)aa.
(iv) λxλy[∀w∀b∀c((Ww & lbw & Cbx & Icw & Ccy) → b = c]aa.
Since (i’) does not entail (ii’), according to DL, (i) does not entail (ii). But it seems that if “□’ in (i) and (ii) represented metaphysical necessity then (i) and (ii) could be paraphrased as (i“) and (ii“) respectively.
(i“) a is necessarily self-identical.
(ii“) a is necessarily identical with a.
However, it is implausible that (i“) does not entail (ii“), and so it seems implausible that □ as interpreted in DL represents metaphysical necessity. This difficulty is independent of the fact that in (i) and (ii) there are occurrences of variables in the scope of □ which are bound by expressions from outside. Suppose that a predicate operator ‘nee’ was given a counterpart-theoretic semantics along the lines proposed in DL. Then (iii) and (iv) would be translated as (iii’) and (iv’) respectively.
(iii) nec λx[x = x]a.
(iii‘) ∀w∀b((Ww & Ibw & Cba) → λx[x = x]b).
(iv) nec λxλy[x = y]aa.
(iv‘) ∀w∀b∀c((Ww & Ibw & Cba & lcw & Cca) → λxλy[x = y]bc).
Since (iii’) does not entail (iv’), according to this proposal, (iii) does not entail (iv). But then, it seems implausible that ‘nee’ in (iii) and (iv) represents metaphysical necessity.
11 Lewis, 45-6
12 Lewis, 45
13 Kaplan, David ‘Demonstratives’ in Almog, JosephPerry, John and Wettstein, Howard eds., Themes from Kaplan (Oxford: Oxford University Press 1989), 481-614Google Scholar
- 1
- Cited by


