Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Borwein, P. B.
and
Chen, Weiyu
1995.
Incomplete rational approximation in the complex plane.
Constructive Approximation,
Vol. 11,
Issue. 1,
p.
85.
2006.
The Mathematica GuideBook for Symbolics.
p.
1.
Hetmaniok, Edyta
Lorenc, Piotr
Pleszczyński, Mariusz
and
Wituła, Roman
2014.
Iterated integrals of polynomials.
Applied Mathematics and Computation,
Vol. 249,
Issue. ,
p.
389.
Pijeira-Cabrera, Hector
and
Rivero-Castillo, Daniel
2020.
Iterated Integrals of Jacobi Polynomials.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 43,
Issue. 3,
p.
2745.
Bello-Hernández, Manuel
Pijeira-Cabrera, Héctor
and
Rivero-Castillo, Daniel
2020.
Iterated Integrals and Borwein–Chen–Dilcher Polynomials.
Mediterranean Journal of Mathematics,
Vol. 17,
Issue. 5,


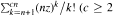 an integer) converge to pieces of a circle and of two "Szegö curves".
an integer) converge to pieces of a circle and of two "Szegö curves".