Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:55:39.086Z Has data issue: false hasContentIssue false
  • English
  • Français

Zero-Dimensional Compactifications of Locally Compact Spaces

Published online by Cambridge University Press:  20 November 2018

R. Grant Woods
R. Grant Woods*
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a locally compact Hausdorff topological space. A compactification of X is a compact Hausdorff space which contains X as a dense subspace. Two compactifications αX and γX of X are equivalent if there is a homeomorphism from αX onto γX that fixes X pointwise. We shall identify equivalent compactifications of a given space. If 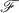is a family of compactifications of X, we can partially order 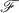by saying that αX ≦ γX if there is a continuous map from γX onto αX that fixes X pointwise.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 4 , August 1974 , pp. 920 - 930
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Fan, K. and Gottesman, N., On compactifications of Freudenthal and Wallrnan, Indag. Math. 14 (1952), 504–510.Google Scholar
2. Filippov, N. D., Projectivity of lattices (Russian), Mat. Sb. 70 (112) 1966, 36-54; Amer. Math. Soc. Transi. 96 (1970), 37–58.Google Scholar
3. Freudenthal, H., Kompaktisierungen und Bikompaktisierungen, Indag. Math. 13 (1951), 184–192.Google Scholar
4. Gillman, L. and Jerison, M., Rings of continuous functions (Van Nostrand, New York, 1960).Google Scholar
5. Gleason, A. M., Projective topological spaces, Illinois J. Math. 2 (1958), 482–489.Google Scholar
6. Gr, G.âtzer, K. Koh, and M. Makkai, On the lattice of subalgebras of a Boolean algebra, Proc. Amer. Math. Soc. 86 (1972), 87–92.Google Scholar
7. Kelley, J., General topology (Van Nostrand, New York, 1955).Google Scholar
8. Magill, K. D., Jr., The lattice of compactifications of a locally compact space, Proc. Lond. Math. Soc. 18 (1968), 231–244.Google Scholar
9. Magill, K. D., Jr. and Glasenapp, J. A., 0-dimensional compactifications and Boolean rings, J. Austral. Math. Soc. 8 (1968), 755–765.Google Scholar
10. Njåstad, O., On Wallman-type compactifications, Math. Z. 91 (1966), 267–276.Google Scholar
11. Sachs, D., The lattice of subalgebras of a Boolean algebra, Can. J. Math. 14 (1962), 451–460.Google Scholar
12. Sikorski, R., Boolean algebras (Springer, New York, second edition, 1964).Google Scholar
13. Strauss, D. P., Extremally disconnected spaces, Proc. Amer. Math. Soc. 18 (1967), 305–309.Google Scholar
14. Thrivikraman, T., On the lattices of compactifications, J. Lond. Math. Soc. 4 (1972), 711–717.Google Scholar
15. Woods, R. G., Co-absolutes of remainders of Stone-Cech compactifications, Pacific J. Math. 37 (1971), 545–560.Google Scholar
16. Woods, R. G., Ideals of pseudocompact regular closed sets and absolutes of Hewitt realcompactifications, General Topology and Appl. 2 (1972), 315–331.Google Scholar