Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:27:27.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted Subspaces of Hardy Spaces

Published online by Cambridge University Press:  20 November 2018

Hong Oh Kim  and
Ern Geun Kwon
Hong Oh Kim
Affiliation:
Korea Advanced Institute of Science and Technology, Seoul, Korea
Ern Geun Kwon
Affiliation:
Korea Advanced Institute of Science and Technology, Seoul, Korea
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A function f in Hp on the unit disc U of the complex plane has the uniform growth

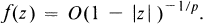
We consider in this paper a subspace 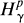of Hp with better uniform growth

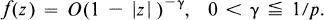
For the previous results on 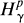see [5, 6, 7]. We start with proving an inequality on Hp which is related to the Hardy-Stein identity (Theorem 2.1) in Section 2. This is applied in the subsequent section to prove some space imbedding theorems related to 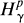(Theorems 3.1 and 3.5). These theorems have some known theorems as their corollaries. Finally we prove some coefficient relations on 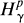in the last section.

The authors wish to thank Professor Patrick Ahern for the helpful conversations during his visit to Korea. Actually he suggested to the first author the possibility of Theorem 2.1 some years ago.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 5 , 01 October 1988 , pp. 1074 - 1083
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Ahern, P. and JevtićM., M., Duality and multipliers for mixed norm spaces, Michigan Math J. 30 (1983), 53–63.Google Scholar
2. Duren, P. L., Theory of Hp spaces (Academic Press, New York, 1970).Google Scholar
3. Flett, T. M., The dual of an inequality of Hardy and Littlewood and some related inequalities, J. Math. Analysis and Appl. 38 (1972), 746–765.Google Scholar
4. Hayman, W. K., Multivalent functions (Cambridge Univ. Press, London, 1958).Google Scholar
5. Kim, H. O., Derivatives of Biaschke products, Pacific J. Math. 114 (1984), 175–191.Google Scholar
6. Kim, H. O., Kim, S. M. and Kwon, E. G., A note on a space Hp,a of holomorphic functions, Bull. Australian Math. Soc. 35 (1987), 471–479.Google Scholar
7. Kim, H. O., Kim, S. M. and Kwon, E. G., A note on the space Hp,a , Comm. Korean Math. Soc. 2 (1987), 47–52.Google Scholar
8. Kwon, E. G., A note on the coefficients of mixed normed spaces, Bull. Australian Math. Soc. 33 (1986), 253–260.Google Scholar
9. Littlewood, J. E. and Paley, R. E. A. C., Theorems on Fourier series and power series (II), Proc. London Math. Soc. (2) 42 (1937), 52–89.Google Scholar
10. Mateljević, M. and Pavlovic, M., Lp-behavior of power series with positive coefficients and Hardy spaces, Proc. Amer. Math. Soc. 87 (1983), 309–316.Google Scholar
11. Stein, P., On a theorem of Riesz, J. London Math. Soc. 8 (1933), 242–247.Google Scholar
12. Zygmund, A., Trigonometric series, 2nd rev. ed. (Cambridge Univ. Press, New York, 1959).Google Scholar