Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T02:33:43.605Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted Norm Inequalities for Fractional Integral Operators With Rough Kernel

Published online by Cambridge University Press:  20 November 2018

Yong Ding  and
Shanzhen Lu
Yong Ding
Affiliation:
Department of Mathematics Beijing Normal UniversityBeijing 100875 China, e-mail: [email protected]
Shanzhen Lu
Affiliation:
Department of Mathematics Beijing Normal UniversityBeijing 100875 China, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

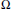Given function $\Omega $ on 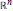${{\mathbb{R}}^{n}}$, we define the fractional maximal operator and the fractional integral operator by

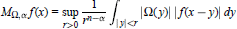$${{M}_{\Omega ,\,\alpha }}f(x)\,=\,_{r>0}^{\sup }\frac{1}{{{r}^{n-\alpha }}}\,\int{{{_{|y|}}_{<r}}\,}|\Omega (y)|\,|f(x-y)|\,dy$$
and
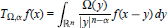$${{T}_{\Omega ,\,\alpha }}f(x)\,=\,\int{_{{{\mathbb{R}}^{n}}}}\,\frac{\Omega (y)}{{{\left| y \right|}^{n-\alpha }}}f(x-y)dy$$
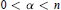 respectively, where $0\,<\,\alpha \,<\,n$. In this paper we study the weighted norm inequalities of 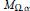${{M}_{\Omega ,\,\alpha }}$ and 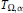${{T}_{\Omega ,\,\alpha }}$ for appropriate 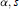$\alpha ,\,s$ and 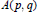$A(p,\,\,q)$ weights in the case that 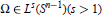$\Omega \,\in \,{{L}^{s}}({{S}^{n-1}})(s>1)$, homogeneous of degree zero.

Keywords

42B2042B25
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 1 , 01 February 1998 , pp. 29 - 39
Copyright
Copyright © Canadian Mathematical Society 1998

References

[BL] Bergh, J. and Löfström, J., Interpolation spaces. An introduction.Springer-Verlag, Berlin, 1976.Google Scholar
[D] Ding, Y., Weak type bounds for a class of rough operators with power weights. Proc. Amer. Math. Soc. 125 (1997), 2939.ndash;2942.Google Scholar
[Du] Duoandikoetxea, J.,Weighted norm inequalities for homogeneous singular integrals. Trans.Amer.Math. Soc. 336 (1993), 869–880.Google Scholar
[GR] Garcia-Cuerva, J. and Rubio, J.L. de Francia, Weighted norm inequalities and related topics.North Holland, Amsterdam, 1985.Google Scholar
[KW] Kurtz, D.S. and Wheeden, R.L., Results on weighted norm inequalities for multipliers. Trans. Amer. Math. Soc. 255 (1979), 343–362.Google Scholar
[MW1] Muckenhoupt, B. and Wheeden, R. L.,Weighted norm inequalities for singular and fractional integrals. Trans. Amer. Math. Soc. 161 (1971), 249–258.Google Scholar
[MW2] Muckenhoupt, B., Weighted norm inequalities for fractional integrals. Trans. Amer. Math. Soc. 192 (1974), 261–27.Google Scholar
[W] Watson, D.K., Weighted estimates for singular integrals via Fourier transform estimates. DukeMath. J. 60 (1990), 389–399.Google Scholar
[We] Welland, G.V., Weighted norm inequalities for fractional integrals. Proc. Amer. Math. Soc. 51 (1975), 143–148.Google Scholar