Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T18:16:18.027Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted Distribution of Low-lying Zeros of GL(2) 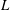$L$-functions

Part of: Zeta and $L$-functions: analytic theory Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  08 January 2019

Andrew Knightly  and
Caroline Reno
Andrew Knightly
Affiliation:
Department of Mathematics and Statistics, University of Maine, Orono, ME 04469-5752, USA Email: [email protected]@maine.edu
Caroline Reno
Affiliation:
Department of Mathematics and Statistics, University of Maine, Orono, ME 04469-5752, USA Email: [email protected]@maine.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that if the zeros of an automorphic 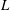$L$-function are weighted by the central value of the 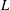$L$-function or a quadratic imaginary base change, then for certain families of holomorphic GL(2) newforms, it has the effect of changing the distribution type of low-lying zeros from orthogonal to symplectic, for test functions whose Fourier transforms have sufficiently restricted support. However, if the 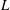$L$-value is twisted by a nontrivial quadratic character, the distribution type remains orthogonal. The proofs involve two vertical equidistribution results for Hecke eigenvalues weighted by central twisted 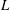$L$-values. One of these is due to Feigon and Whitehouse, and the other is new and involves an asymmetric probability measure that has not appeared in previous equidistribution results for GL(2).

Keywords

low-lying zeroL-function

MSC classification

Primary: 11M41: Other Dirichlet series and zeta functions
Secondary: 11F11: Holomorphic modular forms of integral weight 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 1 , February 2019 , pp. 153 - 182
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This work was partially supported by grant #317659 from the Simons Foundation to author A. K. Section 3 is based in part on the University of Maine MA thesis of author C. R.

References

Barrett, O., Burkhardt, P., DeWitt, J., Dorward, R., and Miller, S. J., One-level density for holomorphic cusp forms of arbitrary level . Res. Number Theory 3(2017), Art. 25. https://doi.org/10.1007/s40993-017-0091-9.Google Scholar
Blomer, V., Buttcane, J., and Raulf, N., A Sato–Tate law for GL(3) . Comment Math. Helv. 89(2014), no. 4, 895–919. https://doi.org/10.4171/CMH/337.Google Scholar
Barnet-Lamb, T., Geraghty, D., Harris, M., and Taylor, R., A family of Calabi-Yau varieties and potential automorphy II . Publ. Res. Inst. Math. Sci. 47(2011), no. 1, 29–98. https://doi.org/10.2977/PRIMS/31.Google Scholar
Bruggeman, R. W., Fourier coefficients of cusp forms . Invent. Math. 45(1978), no. 1, 1–18. https://doi.org/10.1007/BF01406220.Google Scholar
Bruggeman, R. and Miatello, R., Eigenvalues of Hecke operators on Hilbert modular groups . Asian J. Math. 17(2013), no. 4, 729–757. https://doi.org/10.4310/AJM.2013.v17.n4.a10.Google Scholar
Conrey, J. B., Duke, W., and Farmer, D. W., The distribution of the eigenvalues of Hecke operators . Acta Arith. 78(1997), no. 4, 405–409. https://doi.org/10.4064/aa-78-4-405-409.Google Scholar
Feigon, B. and Whitehouse, D., Averages of central L-values of Hilbert modular forms with an application to subconvexity . Duke Math. J. 149(2009), no. 2, 347–410. https://doi.org/10.1215/00127094-2009-041.Google Scholar
File, D., Martin, K., and Pitale, A., Test vectors and central L-values for GL(2) . Algebra Number Theory 11(2017), no. 2, 253–318. https://doi.org/10.2140/ant.2017.11.253.Google Scholar
Gun, S., Murty, M. R., and Rath, P., Summation methods and distribution of eigenvalues of Hecke operators . Funct. Approx. Comment. Math. 39(2008), part 2, 191–204. https://doi.org/10.7169/facm/1229696570.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of integrals, series, and products. 7th ed., Elsevier/Academic Press, San Diego, 2007.Google Scholar
Guo, J., On the positivity of the central critical values of automorphic L-functions for GL(2) . Duke Math. J. 83(1996), no. 1, 157–190. https://doi.org/10.1215/S0012-7094-96-08307-6.Google Scholar
Iwaniec, H., Luo, W., and Sarnak, P., Low lying zeros of families of L-functions . Inst. Hautes Études Sci. Publ. Math. 91(2000), 55–131.Google Scholar
Jackson, J. and Knightly, A., Averages of twisted L-functions . J. Aust. Math. Soc. 99(2015), no. 2, 207–236. https://doi.org/10.1017/S1446788715000142.Google Scholar
Knightly, A. and Li, C., Traces of Hecke operators. Mathematical Surveys and Monographs, 133, American Mathematical Society, Providence, RI, 2006. https://doi.org/10.1090/surv/133.Google Scholar
Knightly, A. and Li, C., Petersson’s trace formula and the Hecke eigenvalues of Hilbert modular forms. In: Modular forms on Schiermonnikoog, Cambridge University Press, Cambridge, 2008. https://doi.org/10.1017/CBO9780511543371.011.Google Scholar
Knightly, A. and Li, C., Weighted averages of modular L-values . Trans. Amer. Math. Soc. 362(2010), no. 3, 1423–1443. https://doi.org/10.1090/S0002-9947-09-04923-X.Google Scholar
Knightly, A. and Li, C., Kuznetsov’s formula and the Hecke eigenvalues of Maass forms . Mem. Amer. Math. Soc. 224(2013), no. 1055. https://doi.org/10.1090/S0065-9266-2012-00673-3.Google Scholar
Kowalski, E., Families of cusp forms. In: Actes de la Conférence “Théorie des Nombres et Applications”, Publ. Math. Besançon Algèbre Théorie Nr., Presses Univ. Franche-Comté, Besançon, 2013, pp. 5–40.Google Scholar
Katz, N. and Sarnak, P., Random mtrices, Frobenius eigenvalues and monodromy. American Mathematical Society Colloquium Publications, 45, American Mathematical Society, Providence, RI, 1999.Google Scholar
Katz, N. and Sarnak, P., Zeros of zeta functions and symmetries . Bull. Amer. Math. Soc. 36(1999), 1–26. https://doi.org/10.1090/S0273-0979-99-00766-1.Google Scholar
Kowalski, E., Saha, A., and Tsimerman, J., Local spectral equidistribution for Siegel modular forms and applications . Compos. Math. 148(2012), no. 2, 335–384. https://doi.org/10.1112/S0010437X11007391.Google Scholar
Li, C., Kuznietsov trace formula and weighted distribution of Hecke eigenvalues . J. Number Theory 104(2004), no. 1, 177–192. https://doi.org/10.1016/S0022-314X(03)00149-5.Google Scholar
Li, C., On the distribution of Satake parameters of GL 2 holomorphic cuspidal representations . Israel J. Math. 169(2009), 341–373. https://doi.org/10.1007/s11856-009-0014-0.Google Scholar
Michel, P. and Ramakrishnan, D., Consequences of the Gross-Zagier formulae: stability of average L-values, subconvexity, and non-vanishing mod p . Number theory, analysis and geometry, Springer, New York, 2012, pp. 437–459. https://doi.org/10.1007/978-1-4614-1260-1_20.Google Scholar
Miller, S. J., An orthogonal test of the L-functions ratios conjecture . Proc. Lond. Math. Soc. (3) 99(2009), no. 2, 484–520. https://doi.org/10.1112/plms/pdp009.Google Scholar
Murty, R. and Sinha, K., Effective equidistribution of eigenvalues of Hecke operators . J. Number Theory 129(2009), no. 3, 681–714. https://doi.org/10.1016/j.jnt.2008.10.010.Google Scholar
Matz, J. and Templier, N., Sato–Tate equidistribution for families of Hecke-Maass forms on $\text{SL}(n,\mathbf{R})/\text{SO}(n)$ . arxiv:1505.07285.Google Scholar
Nagoshi, H., Distribution of Hecke eigenvalues . Proc. Amer. Math. Soc. 134(2006), no. 11, 3097–3106. https://doi.org/10.1090/S0002-9939-06-08709-0.Google Scholar
Newman, M., Integral matrices. Pure and Applied Mathematics, 45, Academic Press, New York-London, 1972.Google Scholar
Ramakrishnan, D. and Rogawski, J., Average values of modular L-series via the relative trace formula . Pure Appl. Math. Q. 1(2005), no. 4, 701–735. https://doi.org/10.4310/PAMQ.2005.v1.n4.a1.Google Scholar
Ramakrishnan, D. and Rogawski, J., Erratum: Average values of modular L-series via the relative trace formula . Pure Appl. Math. Q. 5(2009), no. 4, 1469. https://doi.org/10.4310/PAMQ.2009.v5.n4.a10.Google Scholar
Sarnak, P., Statistical properties of eigenvalues of the Hecke operators. In: Analytic number theory and Diophantine problems (Stillwater, OK, 1984), Progr. Math., 70, Birkhäuser, Boston, MA, 1987, pp. 321–331.Google Scholar
Serre, J.-P., Répartition asymptotique des valeurs propres de l’opérateur de Hecke T p . J. Amer. Math. Soc. 10(1997), no. 1, 75–102. https://doi.org/10.1090/S0894-0347-97-00220-8.Google Scholar
Shin, S. W. and Templier, N., Sato–Tate theorem for families and low-lying zeros of automorphic L-functions . Invent. Math. 203(2016), no. 1, 1–177. https://doi.org/10.1007/s00222-015-0583-y.Google Scholar
Sugiyama, S., Asymptotic behaviors of means of central values of automorphic L-functions for GL(2) . J. Number Theory 156(2015), 195–246. https://doi.org/10.1016/j.jnt.2015.04.003.Google Scholar
Sugiyama, S. and Tsuzuki, M., Relative trace formulas and subconvexity estimates of L-functions for Hilbert modular forms . Acta Arith. 176(2016), no. 1, 1–63.Google Scholar
Tsuzuki, M., Spectral means of central values of automorphic L-functions for GL(2) . Mem. Amer. Math. Soc. 235(2015), no. 1110. https://doi.org/10.1090/memo/1110.Google Scholar
Wang, Y., The quantitative distribution of Hecke eigenvalues . Bull. Aust. Math. Soc. 90(2014), 28–36. https://doi.org/10.1017/S0004972714000070.Google Scholar
Zhou, F., Weighted Sato–Tate vertical distribution of the Satake parameter of Maass forms on PGL(N) . Ramanujan J. 35(2014), no. 3, 405–425. https://doi.org/10.1007/s11139-013-9535-6.Google Scholar