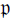Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-23T12:29:09.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak Explicit Matching for Level Zero Discrete Series of Unit Groups of $\mathfrak{p}$-Adic Simple Algebras

Published online by Cambridge University Press:  20 November 2018

Allan J. Silberger  and
Ernst-Wilhelm Zink
Allan J. Silberger
Affiliation:
Cleveland State University, Cleveland, Ohio 44115, USA, email: [email protected]
Ernst-Wilhelm Zink
Affiliation:
Humboldt-Universität, Institut für Mathematik, Rudower Chaussee 25, 10099 Berlin, Germany, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 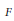$F$ be a 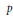$p$-adic local field and let 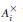$A_{i}^{\times }$ be the unit group of a central simple 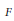$F$-algebra 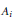${{A}_{i}}$ of reduced degree 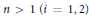$n\,>\,1\,(i\,=\,1,\,2)$. Let 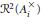${{\mathcal{R}}^{2}}\left( A_{i}^{\times } \right)$ denote the set of irreducible discrete series representations of 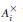$A_{i}^{\times }$. The “Abstract Matching Theorem” asserts the existence of a bijection, the “Jacquet-Langlands” map, 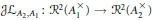$J{{L}_{{{A}_{2}},{{A}_{1}}}}\,:\,{{R}^{2}}\left( A_{1}^{\times } \right)\,\to \,{{R}^{2}}\left( A_{2}^{\times } \right)$ which, up to known sign, preserves character values for regular elliptic elements. This paper addresses the question of explicitly describing the map 𝒥ℒ, but only for “level zero” representations. We prove that the restriction 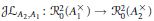$J{{L}_{{{A}_{2}},{{A}_{1}}}}\,:\,R_{0}^{2}\left( A_{1}^{\times } \right)\,\to \,R_{0}^{2}\left( A_{2}^{\times } \right)$ is a bijection of level zero discrete series (Proposition 3.2) and we give a parameterization of the set of unramified twist classes of level zero discrete series which does not depend upon the algebra 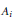${{A}_{i}}$ and is invariant under 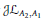$J{{L}_{{{A}_{2}},{{A}_{1}}}}$ (Theorem 4.1).

Keywords

22E5011R39
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 2 , 01 April 2003 , pp. 353 - 378
Copyright
Copyright © Canadian Mathematical Society 2003

References

[Ba] Badulescu, A., Correspondance entre GLn et ses formes intérieures en caractéristique positive. Thèse présentée pour obtenir le grade de Docteur en Sciences, Université de Paris-Sud, Centre d'Orsay, 1999.Google Scholar
[BD] Bernstein, J. (rédigé par P. Deligne), Le .centre. de Bernstein. In: Représentations des groupes réductifs sur un corps local, collection dirig ée par Jean Dieudonné, Hermann, Paris, 1984, 1–32.Google Scholar
[BR] Bernstein, J. and Rumelhart, C., Lectures on Representations of Reductive p-adic Groups. Manuscript, 1996.Google Scholar
[Bo] Borel, A., Admissible Representations of a Semi-Simple Group over a Local Field with Vectors Fixed under an Iwahori Subgroup. Invent.Math. 35 (1976), 233–259.Google Scholar
[BK1] Bushnell, C. and Kutzko, P., The Admissible Dual of GL(N) via Compact Open Subgroups. Annals of Math. Stud. 129, Princeton University Press, Princeton, NJ, 1993.Google Scholar
[BK2] Bushnell, C. and Kutzko, P., Smooth Representations of Reductive p-adic Groups: Structure Theory via Types. Proc. London Math. Soc. 77 (1998), 582–634.Google Scholar
[DKV] Deligne, P., Kazhdan, D. and Vigneras, M.-F., Représentations des algèbres centrales simples p-adiques. In: Représentations des groupes réductifs sur un corps local, collection dirigée par Jean Dieudonné, Hermann, Paris, 1984, 33–117.Google Scholar
[DM] Digne, F. and Michel, J., Representations of Finite Groups of Lie Type. London Mathematical Society Student Texts 21, Cambridge University Press, Cambridge, 1991.Google Scholar
[GSZ] Grabitz, M., Silberger, A., and Zink, E.-W., Level Zero Types and Hecke Algebras for Local Central Simple Algebras. J. Number Theory 91 (2001), 92–125.Google Scholar
[Gr] Green, J., The characters of the finite general linear groups. Trans. Amer.Math. Soc. 80 (1955), 402–447.Google Scholar
[HC] Harish-Chandra, , A Submersion Principle and Its Applications. In: Harish-Chandra Collected Papers, vol. IV, Springer, New York, 1984, 439–446.Google Scholar
[Ro] Rogawski, J., Representations of GL(n) and division algebras over a p-adic field. Duke Math. J. 50 (1983), 161–169.Google Scholar
[SZ] Silberger, A. and Zink, E.-W., The Characters of the Generalized Steinberg Representations of Finite General Linear Groups on the Regular Elliptic Set. Trans. Amer.Math. Soc. 352 (2000), 3339–3356.Google Scholar
[Ze] Zelevinsky, A., Induced Representations of Reductive p-adic Groups II. Ann. Sci. É cole Norm. Sup. (4) 13 (1980), 165–210.Google Scholar