Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T02:37:47.339Z Has data issue: false hasContentIssue false
  • English
  • Français

A Voronovskaya Theorem for Variation-Diminishing Spline Approximation

Published online by Cambridge University Press:  20 November 2018

M. J. Marsden
M. J. Marsden*
Affiliation:
University of Pittsburgh, Pittsburgh, Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [7] Schoenberg introduced the following variation-diminishing spline approximation methods.

Let m > 1 be an integer and let Δ = {xi} be a biinfinite sequence of real numbers with xi ≧ xi + l < xi+m. To a function f associate the spline function Vf of order m with knots Δ defined by

(1.1)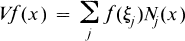

where

and the Nj(x) are B-splines with support xj < x < xj+m normalized so that ΣjNj(x) = 1. See, e.g., [2] for a precise definition of the Nj(x) and a discussion of the properties of Vf.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 5 , 01 October 1986 , pp. 1081 - 1093
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Bajsanski, B. and Bojanic, R., A note on approximation by Bernstein polynomials, Bull. Am. Math. Soc. 70 (1964), 675–677.Google Scholar
2. de Boor, C., A practical guide to splines, Applied Math. Sciences 27 (Springer-Verlag, New York, 1978).CrossRefGoogle Scholar
3. DeVore, R., The approximation of continuous functions by positive linear operators, Lecture Notes in Mathematics 293 (Springer-Verlag, Berlin, 1972).CrossRefGoogle Scholar
4. Lorentz, G. G., Bernstein polynomials (U. of Toronto Press, Toronto, 1953).Google Scholar
5. Marsden, M. J., An identity for spline functions with applications to variation-diminishing spline approximation, J. Approximation Theory 3 (1970), 7–49.Google Scholar
6. Marsden, M. J. and Riemenschneider, S. D., Asymptotic formulae for variation-diminishing splines, in second Edmonton Conference on Approximation Theory, CMS/AMS Conference Proceedings 3 (American Mathematical Society, Providence, 1983), 255–261.Google Scholar
7. Schoenberg, I. J., On spline functions, In Inequalities (Academic Press, New York, 1967), 255–291.Google Scholar