Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T20:13:52.919Z Has data issue: false hasContentIssue false
  • English
  • Français

Verma Modules over Quantum Torus Lie Algebras

Published online by Cambridge University Press:  20 November 2018

Rencai Lü  and
Kaiming Zhao
Rencai Lü
Affiliation:
Department of Mathematics, Suzhou University, Suzhou 215006, Jiangsu, P.R. China, e-mail: [email protected]
Kaiming Zhao
Affiliation:
Department of Mathematics, Wilfrid Laurier University, Waterloo, ON, Canada N2L 3C5 and Institute of Mathematics, Academy ofMathematics and System Sciences, Chinese Academy of Sciences, Beijing 100190, P.R. China, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Representations of various one-dimensional central extensions of quantum tori (called quantum torus Lie algebras) were studied by several authors. Now we define a central extension of quantum tori so that all known representations can be regarded as representations of the new quantum torus Lie algebras 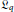${{\mathfrak{L}}_{q}}$. The center of 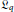${{\mathfrak{L}}_{q}}$ now is generally infinite dimensional.

In this paper, $\mathbb{Z}$-graded Verma modules $\tilde{V}\left( \varphi \right)$ over 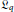${{\mathfrak{L}}_{q}}$ and their corresponding irreducible highest weight modules 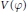$V\left( \varphi \right)$ are defined for some linear functions 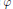$\varphi $. Necessary and sufficient conditions for 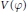$V\left( \varphi \right)$ to have all finite dimensional weight spaces are given. Also necessary and sufficient conditions for Verma modules $\tilde{V}\left( \varphi \right)$ to be irreducible are obtained.

Keywords

17B1017B6517B68
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 2 , 01 April 2010 , pp. 382 - 399
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Berman, S., Gao, Y., and Krylyuk, Y. S., Quantum tori and the structure of elliptic quasi-simple Lie algebras. J. Funct. Anal. 135(1996), no. 2, 339–389. doi:10.1006/jfan.1996.0013Google Scholar
[2] Berman, S. and Billig, Y., Irreducible representations for toroidal Lie algebras. J. Algebra 221(1999), no.1, 188–231. doi:10.1006/jabr.1999.7961Google Scholar
[3] Berman, S. and Szmigielski, J., Principal realization for the extended affine Lie algebra of type with coordinates in a simple quantum torus with two generators. In: Recent Developments in Quantum Affine Algebras and Related Topics. Contemp. Math. 248, American Mathematical Society, Providence, RI, 1999, pp. 39–67.Google Scholar
[4] Billig, Y., Representations of toroidal Lie algebras and Lie algebras of vector fields. Resenhas 6(2004), no. 2-3, 111–119.Google Scholar
[5] Billig, Y., A category of modules for the full toroidal Lie algebra. Int. Math. Res. Not. 2006Art. ID 68395.Google Scholar
[6] Billig, Y., Representations of toroidal extended affine Lie algebras. J. Algebra 308(2007), no. 1, 252–269. doi:10.1016/j.jalgebra.2006.09.010Google Scholar
[7] Billig, Y. and Zhao, K., Weight modules over exp-polynomial Lie algebras. J. Pure Appl. Algebra 191(2004), no. 1-2, 23–42. doi:10.1016/j.jpaa.2003.12.004Google Scholar
[8] Billig, Y. and Zhao, K., Vertex operator representations of quantum tori at roots of unity. Commun. Contemp. Math. 6(2004), no. 1, 195–220. doi:10.1142/S0219199704001252Google Scholar
[9] Brualdi, R.A., Introductory Combinatorics, Second edition. North-Holland Publishing, New York, 1992.Google Scholar
[10] Di Francesco, P., Mathieu, P., and Sénéchal, D., Conformal Field Theory. Springer-Verlag, New York, 1997.Google Scholar
[11] Eswara Rao, S., Irreducible representations for toroidal Lie-algebras. J. Pure Appl. Algebra 202(2005), no. 1-3, 102–117. doi:10.1016/j.jpaa.2005.01.011Google Scholar
[12] Eswara Rao, S. and Moody, R. V., Vertex representations for n-toroidal Lie algebras and a generalization of the Virasoro algebra. Comm. Math. Phys. 159(1994), no. 2, 239–264. doi:10.1007/BF02102638Google Scholar
[13] Eswara Rao, S. and Zhao, K., Highest weight irreducible representations of rank 2 quantum tori. Math. Res. Lett. 11(2004). no.5-6, 615–628.Google Scholar
[14] Eswara Rao, S. and Jiang, C., Classification of irreducible integrable representations for the full toroidal Lie algebras. J. Pure Appl. Algebra 200(2005), no.1-2, 71–85. doi:10.1016/j.jpaa.2004.12.051Google Scholar
[15] Fu, J. and Jiang, C., Integrable representations for the twisted full toroidal Lie algebras. J. Algebra 307(2007), no. 2, 769–794. doi:10.1016/j.jalgebra.2006.08.031Google Scholar
[16] Gao, Y., Representations of extended affine Lie algebras coordinatized by certain quantum tori. Compositio Math. 123(2000), no. 1, 1–25. doi:10.1023/A:1001830622499Google Scholar
[17] Gao, Y., Vertex operators arising from the homogeneous realization for bglN. Comm. Math. Phys. 211(2000), no. 3, 745–777. doi:10.1007/s002200050834Google Scholar
[18] Golenishcheva-Kutuzova, M. and Lebedev, D., Vertex operator representation of some quantum tori Lie algebras. Comm. Math. Phys. 148(1992), no. 2, 403–416. doi:10.1007/BF02100868Google Scholar
[19] Hungerford, T.W., Algebra. Graduate Texts in Mathematics 73. Springer-Verlag, New York, 1980.Google Scholar
[20] Jiang, C. and Jiang, Q., Irreducible representations for the abelian extension of the Lie algebra of diffeomorphisms of tori in dimensions greater than 1. Pacific J. Math. 231(2007), no. 1, 85–101.Google Scholar
[21] Lin, W. and Tan, S., Harish-Chandra modules for the q-analog Virasoro-like algebra. J. Algebra 297(2006), no. 1, 254–272. doi:10.1016/j.jalgebra.2005.09.010Google Scholar
[22] Mc Connell, J. C. and Pettit, J. J., Crossed products and multiplicative analogues of Weyl algebras. J. London Math. Soc. 38(1988), no. 1, 47–55. doi:10.1112/jlms/s2-38.1.47Google Scholar
[23] Zhao, K., Weyl type algebras from quantum tori. Commun. Contemp. Math. 8(2006), no. 2, 135–165. doi:10.1142/S0219199706002064Google Scholar