Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-22T19:49:44.131Z Has data issue: false hasContentIssue false
  • English
  • Français

Upper Bounds on |L(1, χ)| and Applications

Published online by Cambridge University Press:  20 November 2018

Stéphane Louboutin
Stéphane Louboutin*
Affiliation:
Université de Caen, UFR Sciences, Département de Mathématiques, 14032 Caen cedex, France
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

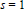We give upper bounds on the modulus of the values at $s\,=\,1$ of Artin $L$-functions of abelian extensions unramified at all the infinite places. We also explain how we can compute better upper bounds and explain how useful such computed bounds are when dealing with class number problems for 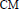$\text{CM}$-fields. For example, we will reduce the determination of all the non-abelian normal 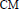$\text{CM}$-fields of degree 24 with Galois group 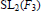$\text{S}{{\text{L}}_{\text{2}}}\left( {{F}_{3}} \right)$ (the special linear group over the finite field with three elements) which have class number one to the computation of the class numbers of 23 such 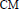$\text{CM}$-fields.

Keywords

11M2011R4211Y3511R29Dedekind zeta functionDirichlet seriesCM-fieldrelative class number
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 4 , 01 August 1998 , pp. 794 - 815
Copyright
Copyright © Canadian Mathematical Society 1998

References

[CK] Chang, K.-Y. and Kwon, S. H., On the imaginary cyclic number fields. (1997), submitted, preprint.Google Scholar
[CMBP] Carletti, E., Monti Bragadin, G. and Perelli, A., On general L-functions. Acta Arith. 66(1994), 147–179.Google Scholar
[Gra] Gras, M. N., Méthodes et algorithmes pour le calcul num érique du nombre de classes et des unités des extensions cubiques cycliques de Q. J. Reine Angew. Math. 277(1975), 89–116.Google Scholar
[Jut1] Jutila, M., On character sums and class numbers. J. Number Theory 5(1973), 203–214.Google Scholar
[Jut2] Jutila, M., On the mean value of L( 1 /2, χ) for real characters. Analysis 1(1981), 149–161.Google Scholar
[Kis] Kisilevski, H., Number fields with class number congruent to 4mod 8 and Hilbert's theorem 94. J. Number Theory 8(1976), 271–279.Google Scholar
[Lef] Lefeuvre, Y., Corps à multiplication complexe diédraux principaux. Univ. Caen, 1997. preprint.Google Scholar
[LLO] Lemmermeyer, F., Louboutin, S. and Okazaki, R., The class number one problem for some non-abelian normal CM-fields of degree 24. to be submitted, preprint.Google Scholar
[LO] Louboutin, S. and Okazaki, R., The class number one problem for some non-abelian normal CM-fields of 2-power degrees. Proc. London Math. Soc., to appear.Google Scholar
[LOO] Louboutin, S., Okazaki, R. and Olivier, M., The class number one problem for some non-abelian normal CM-fields. Trans. Amer.Math. Soc. 349(1997), 3657–3678.Google Scholar
[Lou1] Louboutin, S., Majorations explicites de |L(1, χ)| (suite). C. R. Acad. Sci. Paris 323(1996), 443–446.Google Scholar
[Lou2] Louboutin, S., Computation of relative class number of CM-fields. Math. Comp. 219(1997), 1185–1194.Google Scholar
[Lou3] Louboutin, S., Majorations explicites du résidu au point 1 des fonctions zêta des corps de nombres. J. Math. Soc. Japan 50(1998), 57–69.Google Scholar
[Lou4] Louboutin, S., Explicit bounds for residues of Dedekind zeta functions and relative class numbers. Univ. Caen, 1997. submitted, preprint.Google Scholar
[Was] Washington, L. C., Introduction to Cyclotomic Fields. Grad. Texts in Math. 83, Springer-Verlag.Google Scholar
[WB] Williams, H. C. and Broere, J., A computational technique for evaluating L(1Ò ü) and the class number of a real quadratic fields. Math. Comp. 30(1976), 887–893.Google Scholar