Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bshouty, D.
and
Hengartner, W.
1993.
Univalent solutions of the dirichlet problem for ring domains.
Complex Variables, Theory and Application: An International Journal,
Vol. 21,
Issue. 3-4,
p.
159.
Duren, Peter
and
Hengartner, Walter
1997.
Harmonic mappings of multiply connected domains.
Pacific Journal of Mathematics,
Vol. 180,
Issue. 2,
p.
201.
Lyzzaik, Abdallah
2001.
Quasihomeomorphisms and univalent harmonic mappings onto punctured bounded convex domains.
Pacific Journal of Mathematics,
Vol. 200,
Issue. 1,
p.
159.
Duren, Peter
2004.
Harmonic Mappings in the Plane.
Bshouty, D.
and
Hengartner, W.
2005.
Geometric Function Theory.
Vol. 2,
Issue. ,
p.
479.
Bezrodnykh, S. I.
and
Vlasov, V. I.
2014.
On a Problem of the Constructive Theory of Harmonic Mappings.
Journal of Mathematical Sciences,
Vol. 201,
Issue. 6,
p.
705.


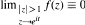 .
.