Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-05T11:58:45.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Units in Group Rings of Free Products of Prime Cyclic Groups

Published online by Cambridge University Press:  20 November 2018

Michael A. Dokuchaev  and
Maria Lucia Sobral Singer
Michael A. Dokuchaev
Affiliation:
Departamento de Matemática Universidade de São Paulo Caixa Postal 66281 São Paulo, SP 05315-970–Brazil, e-mail: [email protected], e-mail: [email protected]
Maria Lucia Sobral Singer
Affiliation:
Departamento de Matemática Universidade de São Paulo Caixa Postal 66281 São Paulo, SP 05315-970–Brazil, e-mail: [email protected], e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $G$ be a free product of cyclic groups of prime order. The structure of the unit group 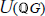$U(\mathbb{Q}G)$ of the rational group ring 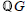$\mathbb{Q}G$ is given in terms of free products and amalgamated free products of groups. As an application, all finite subgroups of 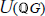$U(\mathbb{Q}G)$, up to conjugacy, are described and the Zassenhaus Conjecture for finite subgroups in 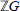$\mathbb{Z}G$ is proved. A strong version of the Tits Alternative for 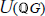$U(\mathbb{Q}G)$ is obtained as a corollary of the structural result.

Keywords

20C0716S3416U6020E06Free ProductsUnits in group ringsZassenhaus Conjecture
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 2 , 01 April 1998 , pp. 312 - 322
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Bovdi, A.A., TheMultiplicative Group of an IntegralGroup Ring. Uzhgorod, Dep. UkrNIINTI, 24.09.87, 2712-Uk87, 1987.Google Scholar
2. Bovdi, A.A., Marciniak, Z. and Sehgal, S.K., Torsion Units in Infinite Group Rings. J. Number Theory 47(1994), 284–299.Google Scholar
3. Dokuchaev, M.A., Finite Subgroups of Units in Integral group Rings. Resenhas IME-USP (3) 2(1996), 293–302.Google Scholar
4. Dokuchaev, M.A. and Juriaans, S.O., Finite Subgroups in Integral Group Rings. Canad. J. Math. (6) 48(1996), 1170–1179.Google Scholar
5. Dokuchaev, M.A., Juriaans, S.O. and Milies, C. Polcino, Integral Group Rings of Frobenius Groups and the Conjectures of H.J. Zassenhaus. Comm. Algebra (7) 25(1997), 2311–2325.Google Scholar
6. Gerasimov, V.N., The group of units of a free product of rings. Math. USSR-Sb. (1) 62(1989), 41–63.Google Scholar
7. Klinger, L., Construction of a counterexample to a conjecture of Zassenhaus. Comm. Algebra 19(1993), 2303–2330.Google Scholar
8. Kurosh, A.G., The theory of groups, II. Chelsea Publ. Co., New York, 1956.Google Scholar
9. Levin, F. and Sehgal, S.K., Zassenhaus conjecture for the infinite dihedral group. ProcAmer.Math. Soc., Special Session, Series in Algebr. 1, World Scientific, Singapore, 1993. 57–68.Google Scholar
10. Lichtman, A.I. and Sehgal, S.K., The elements of finite order in the group of units of group rings of free products of groups. Comm. Algebra 17(1989), 2223–2253.Google Scholar
11. Marciniak, Z.S. and Sehgal, S.K., Zassenhaus Conjecture and Infinite Nilpotent Groups. J. Algebra 184(1996), 207–212.Google Scholar
12. Milies, C. Polcino, Ritter, J. and Sehgal, S.K., On a conjecture of Zassenhaus on torsion units in integralgroup rings II. Proc. Amer.Math. Soc. (2) 97(1986), 206–210.Google Scholar
13. Roggenkamp, K.W. and Taylor, M.J., Group Rings and Class Groups. Birkhäuser Verlag, Basel, 1992.Google Scholar
14. Sehgal, S.K., Units of Integral Group Rings. Longman’s, Essex, 1993.Google Scholar
15. Valenti, A., Torsion Units in Integral Group Rings. Proc. Amer.Math. Soc. (1) 120(1994), 1–4.Google Scholar
16. Weiss, A., Rigidity of p-adic torsion. Ann. Math. 127(1988), 317–332.Google Scholar
17. Weiss, A., Torsion units in integral group rings. J. Reine Angew. Math. 415(1991), 175–187.Google Scholar