Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:12:16.712Z Has data issue: false hasContentIssue false
  • English
  • Français

Unitary Representations of Generalized Symmetric Groups

Published online by Cambridge University Press:  20 November 2018

B. M. Puttaswamaiah
B. M. Puttaswamaiah*
Affiliation:
Carleton University, Ottawa, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper all representations are over the complex field K. The generalized symmetric group S(n, m) of order n!mn is isomorphic to the semi-direct product of the group of n × n diagonal matrices whose rath powers are the unit matrix by the group of all n × n permutation matrices over K. As a permutation group, S(n, m) consists of all permutations of the mn symbols {1, 2, …, mn} which commute with

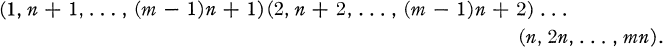
Obviously, S (1, m) is a cyclic group of order m, while S(n, 1) is the symmetric group of order n!. If ci = (i, n+ i, …, (m – 1)n+ i) and

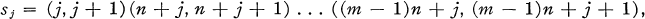
then {c1, c2, …, cn} generate a normal subgroup Q(n) of order mn and {s1, s2, …, sn…1} generate a subgroup S(n) isomorphic to S(n, 1).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 28 - 38
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Clifford, A. H., Representations induced in an invariant subgroup, Ann. of Math. (2) 38 (1937), 533–550.Google Scholar
2. Frame, J. S., Orthogonal group matrices of hyper octahedral groups, Nagoya Math. J. 27 (1966), 585–590.Google Scholar
3. Frame, J. S., Robinson, G. de B., and Thrall, R. M., The hook graphs of the symmetric group, Can. J. Math. 6 (1954), 316–324.Google Scholar
4. Osima, M., On the representations of the generalized symmetric group. I, Math. J. Okayama Univ. 4 (1954), 39–56 Google Scholar
5. Puttaswamaiah, B. M., Alternating and generalized symmetric groups, Thesis, University of Toronto, Toronto, 1963.Google Scholar
6. Robinson, G. de B., Representation theory of the symmetric group, Mathematical Expositions, No. 12 (Univ. Toronto Press, Toronto, 1961).Google Scholar
7. Young, A., On quantitative substitutional analysis. IV; V, Proc. London Math. Soc. (2) 81 (1930), 253–272; 273-288.Google Scholar