Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T01:32:37.394Z Has data issue: false hasContentIssue false
  • English
  • Français

Unit Elements in the Double Dual of a Subalgebra of the Fourier Algebra A(G)

Published online by Cambridge University Press:  20 November 2018

Tianxuan Miao
Tianxuan Miao*
Affiliation:
Department of Mathematical Sciences, Lakehead University, Thunder Bay, Ontario P7E 5E1, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 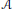$\mathcal{A}$ be a Banach algebra with a bounded right approximate identity and let 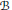$\mathcal{B}$ be a closed ideal of 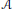$\mathcal{A}$. We study the relationship between the right identities of the double duals 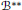${{\mathcal{B}}^{*}}^{*}$ and 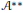${{\mathcal{A}}^{**}}$ under the Arens product. We show that every right identity of 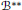${{\mathcal{B}}^{*}}^{*}$ can be extended to a right identity of 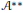${{\mathcal{A}}^{**}}$ in some sense. As a consequence, we answer a question of Lau and Ülger, showing that for the Fourier algebra 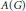$A\left( G \right)$ of a locally compact group 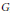$G$, an element 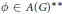$\phi \in A{{\left( G \right)}^{**}}$ is in 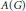$A\left( G \right)$ if and only if 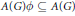$A\left( G \right)\phi \subseteq A\left( G \right)$ and 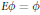$E\phi =\phi$ for all right identities 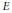$E$ of 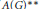$A{{\left( G \right)}^{**}}$. We also prove some results about the topological centers of 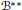${{\mathcal{B}}^{**}}$ and 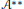${{\mathcal{A}}^{**}}$.

Keywords

43A07compact groupsamenable groupsFourier algebraidentityArens producttopological center.
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 2 , 01 April 2009 , pp. 382 - 394
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Arens, R., The adjoint of a bilinear operation. Proc. Amer. Math. Soc. 2(1951), 839–848.Google Scholar
[2] Baker, J., Lau, A. T., and Pym, J., Module homomorphisms and topological centres associated with weakly sequentially complete Banach algebras. J. Funct. Anal. 158(1998), no. 1, 186–208.Google Scholar
[3] Bonsall, F. F. and Duncan, J., Complete normed algebras. Ergebnisse der Mathmatik und ihrer Grenzgebiete 80, Springer-Verlag, New York-Heidelberg-Berlin, 1973.Google Scholar
[4] Derighetti, A., Filali, M., and Monfared, M. S., On the ideal structure of some Banach algebras related to convolution operators on Lp (G . J. Funct. Anal. 215(2004), no. 2, 341–365.Google Scholar
[5] Eymard, P., L'algèbre de Fourier d'un groupe localement compact. Bull. Soc. Math. France 92(1964), 181–236.Google Scholar
[6] Forrest, B., Arens regularity and discrete groups. Pacific J. Math. 151(1991), no. 2, 217–227.Google Scholar
[7] Granirer, E. E. and Leinert, M., On some topologies which coincide on the unit sphere of the Fourier-Stieltjes algebra B (G ) and of the measure algebra M (G . Rocky Mountain J. Math. 11(1981), no. 3, 459–472.Google Scholar
[8] Herz, C., Harmonic synthesis for subgroups. Ann. Inst. Fourier (Grenoble) 23(1973), no. 3, 91–123.Google Scholar
[9] Hu, Z., Open subgroups and the centre problem for the Fourier algebra. Proc. Amer. Math. Soc. 134(2006), no. 10, 3085–3095.Google Scholar
[10] Hu, Z. and Neufang, M., Decomposability of von Neumann algebras and the Mazur property of higher level. Canad. J. Math. 58(2006), no. 4, 768–795.Google Scholar
[11] Lau, A. T., The second conjugate algebra of the Fourier algebra of a locally compact group. Trans. Amer. Math. Soc. 267(1981), no. 1, 53–63.Google Scholar
[12] Lau, A. T. and Losert, V., The C-algebra generated by operators with compact support on a locally compact group. J. Funct. Anal. 112(1993), no. 1, 1–30.Google Scholar
[13] Lau, A. T. and Ülger, A., Topological centers of certain dual algebras. Trans. Amer. Math. Soc. 348(1996), no. 3, 1191–1212.Google Scholar
[14] Miao, T., Decomposition of B (G . Trans. Amer. Math. Soc. 351(1999), no. 11, 4675–4692.Google Scholar
[15] Miao, T., Characterizations of elements with compact support in the dual spaces of Ap (G )-modules of PMp (G . Proc. Amer. Math. Soc. 132(2004), no. 12, 3671–3678.Google Scholar
[16] Pier, J.-P., Amenable locally compact groups. Pure and Applied Mathematics, John Wiley and Sons, New York, 1984.Google Scholar
[17] Reiter, H. and Stegeman, J. D., Classical harmonic analysis and locally compact groups. Oxford University Press, 2000.Google Scholar