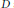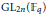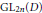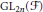Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jiang, Dihua
Nien, Chufeng
and
Qin, Yujun
2008.
Local Shalika models and functoriality.
manuscripta mathematica,
Vol. 127,
Issue. 2,
p.
187.
Jiang, Dihua
Nien, Chufeng
and
Qin, Yujun
2010.
Symplectic supercuspidal representations of GL(2n) overp-adic fields.
Pacific Journal of Mathematics,
Vol. 245,
Issue. 2,
p.
273.
Jiang, DiHua
Nien, ChuFeng
and
Qin, YuJun
2010.
Symplectic supercuspidal representations and related problems.
Science China Mathematics,
Vol. 53,
Issue. 3,
p.
533.
Zhang, Lei
2010.
Gelfand pairs(Sp4n(F),Sp2n(E)).
Journal of Number Theory,
Vol. 130,
Issue. 11,
p.
2428.
Jiang, Dihua
Nien, Chufeng
and
Qin, Yujun
2013.
Generalized Shalika models of p-adic SO4n and functoriality.
Israel Journal of Mathematics,
Vol. 195,
Issue. 1,
p.
135.
Gehrmann, Lennart
2018.
On Shalika models and p-adic L-functions.
Israel Journal of Mathematics,
Vol. 226,
Issue. 1,
p.
237.
Suzuki, Miyu
2018.
Correspondence of models under local theta lifting.
Journal of Algebra,
Vol. 507,
Issue. ,
p.
186.
Beuzart-Plessis, Raphaël
and
Wan, Chen
2019.
A local trace formula for the generalized Shalika model.
Duke Mathematical Journal,
Vol. 168,
Issue. 7,
Chen, Cheng
Jiang, Dihua
Lin, Bingchen
and
Tian, Fangyang
2020.
Archimedean non-vanishing, cohomological test vectors, and standard L-functions of $${\mathrm {GL}}_{2n}$$: real case.
Mathematische Zeitschrift,
Vol. 296,
Issue. 1-2,
p.
479.
Dimitrov, Mladen
Januszewski, Fabian
and
Raghuram, A.
2020.
L-functions of GL2n: p-adic properties and non-vanishing of twists.
Compositio Mathematica,
Vol. 156,
Issue. 12,
p.
2437.