Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T11:21:34.414Z Has data issue: false hasContentIssue false
  • English
  • Français

Unipotent Orbital Integrals of Hecke Functions for GL(n)

Published online by Cambridge University Press:  20 November 2018

Rebecca A. Herb
Rebecca A. Herb*
Affiliation:
Department of Mathematics University of Maryland College Park, Maryland 20742 U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G = GL(n, F) where F is a p-adic field, and let 𝓗(G) denote the Hecke algebra of spherical functions on G. Let u1,..., up denote a complete set of representatives for the unipotent conjugacy classes in G. For each 1 ≤ i ≤ p, let μi be the linear functional on 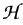such that μi(f) is the orbital integral of f over the orbit of ui. Waldspurger proved that the μi, 1 ≤ i ≤ p, are linearly independent. In this paper we give an elementary proof of Waldspurger's theorem which provides concrete information about the Hecke functions needed to separate orbits. We also prove a twisted version of Waldspurger's theorem and discuss the consequences for SL(n, F).

Keywords

22E35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 2 , 01 April 1994 , pp. 308 - 323
Copyright
Copyright © Canadian Mathematical Society 1994

References

[A-C] Arthur, J. and Clozel, L., Simple Algebras, Base Change, and the Advanced Theory of the Trace Formula, Ann. of Math. Studies 120, Princeton University Press, Princeton, N.J., 1989.Google Scholar
[HI] Hales, T., Unipotent representations and unipotent classes in SL(/i).Google Scholar
[VI] Vignéras, M. F., Characterisation des intégrales orbitales sur un groupe réductif p-adique, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 29(1981), 945–962.Google Scholar
[Wl] Waldspurger, J. L., Sur les germes de Shalika pour les groupes linéaires. Google Scholar
[W2] Waldspurger, J. L.,A propos des intégrales orbitales pour GL(n). Google Scholar