Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T12:23:35.686Z Has data issue: false hasContentIssue false
  • English
  • Français

Unbounded Positive Definite Functions

Published online by Cambridge University Press:  20 November 2018

James Stewart
James Stewart*
Affiliation:
University of London, London, England; McMaster University, Hamilton, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be an abelian group, written additively. A complexvalued function ƒ, defined on G, is said to be positive definite if the inequality

1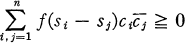

holds for every choice of complex numbers C1, …, cn and S1, …, sn in G. It follows directly from (1) that every positive definite function is bounded. Weil (9, p. 122) and Raïkov (5) proved that every continuous positive definite function on a locally compact abelian group is the Fourier-Stieltjes transform of a bounded positive measure, thus generalizing theorems of Herglotz (4) (G = Z, the integers) and Bochner (1) (G = R, the real numbers).

If ƒ is a continuous function, then condition (1) is equivalent to the condition that

2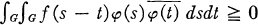

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 1309 - 1318
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Bochner, S., Vorlesungen uber Fourier sche Integrate (Akademische Verlagsgesellschaft, Leipzig, 1932) ; translated by Morris Tenenbaun and Harry Pollard: Lectures on Fourier integrals (with the author's supplement on Monotonie functions, Stieltjes integrals, and harmonic analysis), Annals of Mathematics Studies, No. 42 (Princeton Univ. Press, Princeton, N.J., 1959).Google Scholar
2. Cooper, J. L. B., Positive definite functions of a real variable, Proc. London Math. Soc. (3) 10 (1960), 53–66.Google Scholar
3. Gel'fand, I. M. and Vilenkin, N. Ya., Generalized functions, Vol. 4, Applications of harmonic analysis (Academic Press, New York, 1964).Google Scholar
4. Herglotz, G., Über Potenzreihen mit positiven reelen Teil im Einheitskreis, Leipziger Berichte 63 (1911), 501–511.Google Scholar
5. Raïkov, D. A., Positive definite functions on commutative groups with an invariant measure, C. R. (Doklady) Acad. Sci. URSS (N. S.) 28 (1940), 296–300. (Russian)Google Scholar
6. Rudin, W., Fourier analysis on groups, Interscience Tracts in Pure and Applied Math., No. 12 (Interscience, New York, 1962).Google Scholar
7. Simon, A. B., Cesàro summability on groups: Characterization and inversion of Fourier transforms, pp. 208-215 in Function algebras, Proc. Internat. Sympos. on Function Algebras, Tulane Univ., 1965 (Scott-Foresman, Chicago, Illinois, 1966).Google Scholar
8. Stewart, J. D., Positive definite functions and generalizations, Ph.D. thesis, University of Toronto, Toronto, Ontario, 1967.Google Scholar
9. Weil, André, L'intégration dans les groupes topologiques et ses applications, Actualités Sci. Indust., no. 869 (Hermann, Paris, 1940; revised, 1951).Google Scholar