Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T10:52:20.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Un Théorème De Régularité Pour Une Équation Différentielle Abstraite

Published online by Cambridge University Press:  20 November 2018

Paul Arminjon
Paul Arminjon*
Affiliation:
Université de Montréal, Montréal, Québec
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soit Y un espace localement convexe complet, la topologie étant définie par une famille de semi-normes {pα}. Soit A un opérateur fermé de domaine D(A) dense dans Y. Nous considérons dans cet article des fonctions u de la variable réelle t à valeurs dans Y. On dit que u(t) ∈ Cl[(a, b); Y] est une solution au sens classique de l'équation différentielle abstraite (ou opérationnelle)

(1)

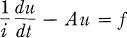
si pour tout t ∈ (a, b), u(t) ∈ D(A), et satisfait la relation

élément de Y, f étant une fonction continue à valeurs dans Y.

Dans leur important mémoire [1], Agmon et Nirenberg ont étudié en détail les propriétés des solutions d'une telle équation dans le cas où Y est un espace de Banach.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 2 , 01 April 1970 , pp. 288 - 296
Copyright
Copyright © Canadian Mathematical Society 1970

References

Bibliographie

1. Agmon, S. et Nirenberg, L., Properties of solutions of ordinary differential equations in Banach space, Comm. Pure Appl. Math. 16 (1963), 121–239.Google Scholar
2. Arminjon, P., Quelques aspects de la théorie des équations différentielles opérationnelles, Thèse, Université de Montréal, Montréal, Québec, 1968.Google Scholar
3. Bourbaki, N., Eléments de mathématique, Fasc. XXV, première partie, Livre VI: Intégration, Chapitre 6: Intégration vectorielle, Actualités Sci. Indust., No. 1281 (Hermann, Paris, 1959).Google Scholar
4. Dunford, N. et Schwartz, J. T., Linear operators, Vol. I (Interscience, New York, 1958).Google Scholar
5. Edwards, R. E., Functional analysis (Holt, Rinehart, and Winston, New York, 1965).Google Scholar
6. Hormander, L., Linear partial differential operators, Die Grundlehren der mathematischen Wissenschaften, Bd. 116 (Academic Press, New York; Springer-Verlag, Berlin, 1963).Google Scholar
7. Köthe, G., Topologische lineare Raiime. I, Die Grundlehren der mathematischen Wissenschaften, Bd. 107 (Springer-Verlag, Berlin, 1960).Google Scholar