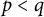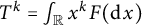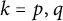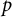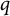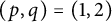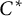1 Introduction
One of the most important concepts in mathematics and physics is the notion of a normalized positive-operator-valued measure (POV measure) also known as a probability-operator-valued measure or a generalized observable, or else semispectral measure. This concept was introduced in the 1940s by Naimark (see [Reference Naimark37–Reference Naimark39]). POV measures play a significant role in operator theory [Reference Akhiezer and Glazman1, Reference Berberian7, Reference Jung and Stochel26, Reference Pietrzycki and Stochel43] and are a standard tool in quantum information theory and quantum optics [Reference Brandt12, Reference Busch, Lahti, Pellonpää and Ylinen13, Reference Holevo23, Reference Vedral53]. Recall that a map
![]() $F\colon \mathscr {A} \to \boldsymbol {B}(\mathcal {H})$
defined on a
$F\colon \mathscr {A} \to \boldsymbol {B}(\mathcal {H})$
defined on a
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathscr {A}$
of subsets of a set
$\mathscr {A}$
of subsets of a set
![]() $X$
is said to be:
$X$
is said to be:
-
• a POV measure if
 $\langle F (\cdot )h, h\rangle $
is a positive measure for every
$\langle F (\cdot )h, h\rangle $
is a positive measure for every
 $h \in \mathcal {H}$
,
$h \in \mathcal {H}$
, -
• a semispectral measure if
 $F$
is a POV measure such that
$F$
is a POV measure such that
 $F(X) = I$
,
$F(X) = I$
, -
• a spectral measure if
 $F$
is a semispectral measure such that
$F$
is a semispectral measure such that
 $F(\varDelta )$
is an orthogonal projection for every
$F(\varDelta )$
is an orthogonal projection for every
 $\varDelta \in \mathscr {A}$
,
$\varDelta \in \mathscr {A}$
,
where
![]() $\boldsymbol {B}(\mathcal {H})$
is the collection of all bounded linear operators on a Hilbert space
$\boldsymbol {B}(\mathcal {H})$
is the collection of all bounded linear operators on a Hilbert space
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $I$
is the identity operator on
$I$
is the identity operator on
![]() $\mathcal {H}$
. The celebrated Naimark’s dilation theorem (see [Reference Naimark39] and [Reference Mlak34, Theorem 6.4]) states that a POV measure
$\mathcal {H}$
. The celebrated Naimark’s dilation theorem (see [Reference Naimark39] and [Reference Mlak34, Theorem 6.4]) states that a POV measure
![]() $F\colon \mathscr {A} \to \boldsymbol {B}(\mathcal {H})$
can always be represented as the
$F\colon \mathscr {A} \to \boldsymbol {B}(\mathcal {H})$
can always be represented as the
![]() $R$
-compression
$R$
-compression
![]() $R^*E(\cdot )R$
of a spectral measure
$R^*E(\cdot )R$
of a spectral measure
![]() $E\colon \mathscr {A} \to \boldsymbol {B}(\mathcal {K})$
, where
$E\colon \mathscr {A} \to \boldsymbol {B}(\mathcal {K})$
, where
![]() $\mathcal {K}$
is a Hilbert space and
$\mathcal {K}$
is a Hilbert space and
![]() $R$
is a bounded linear operator from
$R$
is a bounded linear operator from
![]() $\mathcal {H}$
to
$\mathcal {H}$
to
![]() $\mathcal {K}$
. By [Reference Mlak34, p. 14],
$\mathcal {K}$
. By [Reference Mlak34, p. 14],
![]() $\mathcal {K}$
can be made minimal in the sense that
$\mathcal {K}$
can be made minimal in the sense that
![]() $\mathcal {K} = \bigvee \{E(\varDelta )R(\mathcal {H}) \colon \varDelta \in \mathscr {A}\}$
. If
$\mathcal {K} = \bigvee \{E(\varDelta )R(\mathcal {H}) \colon \varDelta \in \mathscr {A}\}$
. If
![]() $F$
is semispectral, then
$F$
is semispectral, then
![]() $\mathcal {H}$
is a subspace of
$\mathcal {H}$
is a subspace of
![]() $\mathcal {K}$
and
$\mathcal {K}$
and
![]() $R$
is the (isometric) embedding of
$R$
is the (isometric) embedding of
![]() $\mathcal {H}$
into
$\mathcal {H}$
into
![]() $\mathcal {K}$
, and so the minimality condition takes the form
$\mathcal {K}$
, and so the minimality condition takes the form
![]() $\mathcal {K} = \bigvee \{E(\varDelta )\mathcal {H} \colon \varDelta \in \mathscr {A}\}$
.
$\mathcal {K} = \bigvee \{E(\varDelta )\mathcal {H} \colon \varDelta \in \mathscr {A}\}$
.
It turns out that, from a mathematical and physical point of view, it is important to investigate the relationship between semispectral and spectral measures. In the classical von Neumann description of quantum mechanics, self-adjoint operators or, equivalently, Borel spectral measures on the real line represent observables. This approach is insufficient in describing many natural properties of measurements, such as measurement inaccuracy. Therefore, in standard modern quantum theory, the generalization to semispectral measures is widely used. In particular, this is the case in quantum information theory and in quantum optics (to represent measurement statistics). Among the papers undertaking this line of research, the following are noteworthy [Reference Beneduci3–Reference Beneduci and Nisticò6, Reference Cattaneo and Nisticò14, Reference Holevo22, Reference Jenčová and Pulmannová25, Reference Kiukas, Lahti and Ylinen30, Reference Kruszyński and de Muynck31, Reference Naimark37].
By a Borel POV measure on
![]() $\mathbb {R}$
, we mean a POV measure
$\mathbb {R}$
, we mean a POV measure
![]() $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
, where
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
, where
![]() $\mathfrak {B}(\mathbb {R})$
stands for the
$\mathfrak {B}(\mathbb {R})$
stands for the
![]() $\sigma $
-algebra of all Borel subsets of the real line
$\sigma $
-algebra of all Borel subsets of the real line
![]() $\mathbb {R}$
(below, the algebra
$\mathbb {R}$
(below, the algebra
![]() $\boldsymbol {B}(\mathcal {H})$
will not be explicitly mentioned unless necessary). For an integer
$\boldsymbol {B}(\mathcal {H})$
will not be explicitly mentioned unless necessary). For an integer
![]() $n\geqslant 1$
and a Borel POV measure
$n\geqslant 1$
and a Borel POV measure
![]() $F$
on
$F$
on
![]() $\mathbb {R}$
with compact support,Footnote
1
the integral
$\mathbb {R}$
with compact support,Footnote
1
the integral
is a (bounded) self-adjoint operator, which is called the nth operator moment of
![]() $F$
. A straightforward application of the Weierstrass approximation theorem and the uniqueness part of the Riesz representation theorem shows that a normalized Borel POV measure on
$F$
. A straightforward application of the Weierstrass approximation theorem and the uniqueness part of the Riesz representation theorem shows that a normalized Borel POV measure on
![]() $\mathbb {R}$
with compact support is uniquely determined by its operator moments. One of the features of a Borel spectral measure on
$\mathbb {R}$
with compact support is uniquely determined by its operator moments. One of the features of a Borel spectral measure on
![]() $\mathbb {R}$
is the multiplicativity of the corresponding Stone–von Neumann functional calculus. In particular, if
$\mathbb {R}$
is the multiplicativity of the corresponding Stone–von Neumann functional calculus. In particular, if
![]() $E$
is a Borel spectral measure on
$E$
is a Borel spectral measure on
![]() $\mathbb {R}$
with compact support, then the following identities hold:Footnote
2
$\mathbb {R}$
with compact support, then the following identities hold:Footnote
2
Hence, all operator moments of
![]() $E$
are determined by the first one, and according to the spectral theorem, there is a one-to-one correspondence between Borel spectral measures on
$E$
are determined by the first one, and according to the spectral theorem, there is a one-to-one correspondence between Borel spectral measures on
![]() $\mathbb {R}$
and their first operator moments. This is no longer true for general Borel semispectral measures on
$\mathbb {R}$
and their first operator moments. This is no longer true for general Borel semispectral measures on
![]() $\mathbb {R}$
. It turns out, however, that the single equality in (1.1) with
$\mathbb {R}$
. It turns out, however, that the single equality in (1.1) with
![]() $n=2$
guarantees spectrality.
$n=2$
guarantees spectrality.
Theorem 1.1 ([Reference Kruszyński and de Muynck31, Proposition 1], [Reference Kiukas, Lahti and Ylinen30, Theorem 5], and [Reference Pietrzycki and Stochel43, Remark 5.3])
A Borel semispectral measure
![]() $F$
on
$F$
on
![]() $\mathbb {R}$
with compact supportFootnote
3
is spectral if and only if
$\mathbb {R}$
with compact supportFootnote
3
is spectral if and only if
It is worth mentioning that if
![]() $F$
is a Borel semispectral measure on
$F$
is a Borel semispectral measure on
![]() $\mathbb {R}$
with compact support, then the operator
$\mathbb {R}$
with compact support, then the operator
![]() $\mathrm {Var}(F)$
, called (intrinsic) noise operator (see [Reference Busch, Lahti, Pellonpää and Ylinen13, p. 177]), defined as
$\mathrm {Var}(F)$
, called (intrinsic) noise operator (see [Reference Busch, Lahti, Pellonpää and Ylinen13, p. 177]), defined as
is always positive (see Corollary 3.4; this can also be deduced from the Kadison inequality (2.4)). Thus, according to Theorem 1.1, equality holds in
![]() $\mathrm {Var}(F) \geqslant 0$
only for spectral measures.
$\mathrm {Var}(F) \geqslant 0$
only for spectral measures.
In this connection, it is worth emphasizing that Theorem 1.1 was developed for the needs of quantum physics. Namely, the main purpose of the quantization proposed in [Reference Kiukas, Lahti and Ylinen29, Reference Kiukas, Lahti and Ylinen30] was to construct observables that are not spectral measures, and this was done by applying the technique of operator moments. To achieve this goal, it was important to be able to use operator moments to determine whether a given observable is or is not a spectral measure. This led Kiukas, Lahti, and Ylinen to the following question (see [Reference Kiukas, Lahti and Ylinen30, Section VI]; see also [Reference Kiukas28, Section 5]).
Question 1.2 When is a positive operator measure projection valued?
In a recent paper [Reference Pietrzycki and Stochel43], we gave a solution to [Reference Curto, Lee and Yoon16, Problem 1.1] concerning subnormal square roots of quasinormal operators. In fact, the paper [Reference Pietrzycki and Stochel43] provides two solutions to this problem that use two different approaches. The first one appeals to the theory of operator monotone functions, in particular Hansen’s inequality. The second one is based on the technique that utilizes operator moments of semispectral measures. A detailed analysis of both solutions led us to a new criterion for the spectrality of a Borel semispectral measure on
![]() $\mathbb {R}$
compactly supported in
$\mathbb {R}$
compactly supported in
![]() $[0,\infty )$
, written in terms of its two operator moments. This criterion was used to solve a generalization of [Reference Curto, Lee and Yoon16, Problem 1.1] (see [Reference Pietrzycki and Stochel43, Theorem 4.1]).
$[0,\infty )$
, written in terms of its two operator moments. This criterion was used to solve a generalization of [Reference Curto, Lee and Yoon16, Problem 1.1] (see [Reference Pietrzycki and Stochel43, Theorem 4.1]).
Theorem 1.3 ([Reference Pietrzycki and Stochel43, Theorem 4.2] and [Reference Pietrzycki and Stochel44])
Let
![]() $T\in \boldsymbol {B}(\mathcal {H})$
be a positive operator, and let
$T\in \boldsymbol {B}(\mathcal {H})$
be a positive operator, and let
![]() $\alpha ,\beta $
be two distinct positive real numbers. Assume that
$\alpha ,\beta $
be two distinct positive real numbers. Assume that
![]() $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
is a semispectral measure compactly supported in
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
is a semispectral measure compactly supported in
![]() $[0,\infty )$
. Then the following conditions are equivalent:
$[0,\infty )$
. Then the following conditions are equivalent:
-
(i)
 $F$
is the spectral measure of
$F$
is the spectral measure of
 $T$
.
$T$
. -
(ii)
 $T^n = \int _{[0,\infty )} x^n F(\mathrm {d\hspace {.1ex}} x)$
for all integers
$T^n = \int _{[0,\infty )} x^n F(\mathrm {d\hspace {.1ex}} x)$
for all integers
 $n\geqslant 0$
.
$n\geqslant 0$
. -
(iii)
 $T^r = \int _{[0,\infty )} x^r F(\mathrm {d\hspace {.1ex}} x)$
for all
$T^r = \int _{[0,\infty )} x^r F(\mathrm {d\hspace {.1ex}} x)$
for all
 $r \in [0,\infty )$
.
$r \in [0,\infty )$
. -
(iv)
 $T^r =\int _{[0,\infty )} x^r F(\mathrm {d\hspace {.1ex}} x)$
for
$T^r =\int _{[0,\infty )} x^r F(\mathrm {d\hspace {.1ex}} x)$
for
 $r= \alpha , \beta $
.
$r= \alpha , \beta $
.
As shown in the proof of [Reference Pietrzycki and Stochel43, Theorem 4.2], the implication (iv)
![]() $\Rightarrow $
(i) is equivalent to the fact that a semispectral measure
$\Rightarrow $
(i) is equivalent to the fact that a semispectral measure
![]() $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
compactly supported in
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
compactly supported in
![]() $[0,\infty )$
for which there exists
$[0,\infty )$
for which there exists
![]() $s\in (0,\infty ) \backslash \{1\}$
such that
$s\in (0,\infty ) \backslash \{1\}$
such that
is spectral (see [Reference Pietrzycki and Stochel43, Lemma 4.3]).
In view of Question 1.2 and Theorems 1.1 and 1.3, it seems natural to pose the following general problem in which
![]() $\varXi $
is a fixed nonempty set of positive integers (if the set
$\varXi $
is a fixed nonempty set of positive integers (if the set
![]() $\varXi $
is finite, then we always order its elements in a nondecreasing manner). Problem 1.4 can be regarded as a generalization of [Reference Pietrzycki and Stochel43, Problem 5.2], which deals with two-element sets
$\varXi $
is finite, then we always order its elements in a nondecreasing manner). Problem 1.4 can be regarded as a generalization of [Reference Pietrzycki and Stochel43, Problem 5.2], which deals with two-element sets
![]() $\varXi $
.
$\varXi $
.
Problem 1.4 Let
![]() $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
be a semispectral measure with compact support, and let
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
be a semispectral measure with compact support, and let
![]() $T\in \boldsymbol {B}(\mathcal {H})$
be a self-adjoint operator. Does the system of equations
$T\in \boldsymbol {B}(\mathcal {H})$
be a self-adjoint operator. Does the system of equations
imply that
![]() $F$
is spectral?
$F$
is spectral?
This problem can be rephrased equivalently in terms of dilation theory as follows (use Naimark’s dilation theorem and Lemma 3.2).
Problem 1.5 Let
![]() $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
be a semispectral measure with compact support, let
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
be a semispectral measure with compact support, let
![]() $E\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {K})$
be a minimal spectral dilation of
$E\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {K})$
be a minimal spectral dilation of
![]() $F$
(i.e.,
$F$
(i.e.,
![]() $E$
is a spectral measure satisfying (3.2) and (3.4)), let
$E$
is a spectral measure satisfying (3.2) and (3.4)), let
![]() $S$
be the first operator moment of
$S$
be the first operator moment of
![]() $E$
(i.e.,
$E$
(i.e.,
![]() $S=\int _{\mathbb {R}} x E(\mathrm {d\hspace {.1ex}} x)$
), and let
$S=\int _{\mathbb {R}} x E(\mathrm {d\hspace {.1ex}} x)$
), and let
![]() $T\in \boldsymbol {B}(\mathcal {H})$
be a self-adjoint operator. Does the system of equations
$T\in \boldsymbol {B}(\mathcal {H})$
be a self-adjoint operator. Does the system of equations
imply that
![]() $P$
and
$P$
and
![]() $S$
commutes?
$S$
commutes?
It turns out that Problem 1.4 is closely related to the question of multiplicativity of unital positive linear maps on
![]() $C^*$
-algebras (see Remark 4.3). In fact, the two problems are logically equivalent regardless of the cardinality of the set
$C^*$
-algebras (see Remark 4.3). In fact, the two problems are logically equivalent regardless of the cardinality of the set
![]() $\varXi $
(see Remark 4.2). The
$\varXi $
(see Remark 4.2). The
![]() $C^*$
-algebra counterpart of Problem 1.4 takes the following form.
$C^*$
-algebra counterpart of Problem 1.4 takes the following form.
Problem 1.6 Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be unital
$\mathcal {B}$
be unital
![]() $C^*$
-algebras, let
$C^*$
-algebras, let
![]() $\varPhi \colon \mathcal {A} \rightarrow \mathcal {B}$
be a unital positive linear map, and let
$\varPhi \colon \mathcal {A} \rightarrow \mathcal {B}$
be a unital positive linear map, and let
![]() $a\in \mathcal {A}$
and
$a\in \mathcal {A}$
and
![]() $b\in \mathcal {B}$
be self-adjoint. Does the system of equations
$b\in \mathcal {B}$
be self-adjoint. Does the system of equations
imply that
![]() $\varPhi $
restricted to the unital subalgebra generated by
$\varPhi $
restricted to the unital subalgebra generated by
![]() $\{a\}$
is multiplicative?
$\{a\}$
is multiplicative?
The correspondence between Problems 1.4 and 1.5 allows us to use the theories of operator monotone functions and positive linear maps on
![]() $C^*$
-algebras, as well as related operator inequalities, to prove the main results of this paper, which provide complete solutions to Problems 1.4–1.6 for two-element sets
$C^*$
-algebras, as well as related operator inequalities, to prove the main results of this paper, which provide complete solutions to Problems 1.4–1.6 for two-element sets
![]() $\varXi $
. We begin with the affirmative solutions.
$\varXi $
. We begin with the affirmative solutions.
Theorem 1.7 Let
![]() $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
be a semispectral measure with compact support, and let
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
be a semispectral measure with compact support, and let
![]() $p,q$
be positive integers such that
$p,q$
be positive integers such that
![]() $p<q$
,
$p<q$
,
![]() $p$
is odd, and
$p$
is odd, and
![]() $q$
is even. If
$q$
is even. If
![]() $T \in \boldsymbol {B}(\mathcal {H})$
is self-adjoint, then the following conditions are equivalent:
$T \in \boldsymbol {B}(\mathcal {H})$
is self-adjoint, then the following conditions are equivalent:
-
(i)
 $F$
is the spectral measure of
$F$
is the spectral measure of
 $T$
.
$T$
. -
(ii)
 $T^k =\int _{\mathbb {R}} x^k F(\mathrm {d\hspace {.1ex}} x)$
for all integers
$T^k =\int _{\mathbb {R}} x^k F(\mathrm {d\hspace {.1ex}} x)$
for all integers
 $k\geqslant 0$
.
$k\geqslant 0$
. -
(iii)
 $T^k =\int _{\mathbb {R}} x^k F(\mathrm {d\hspace {.1ex}} x)$
for
$T^k =\int _{\mathbb {R}} x^k F(\mathrm {d\hspace {.1ex}} x)$
for
 $k=p, q$
.
$k=p, q$
.
The affirmative solution to Problem 1.6 takes the form.
Theorem 1.8 Let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be unital
$\mathcal {B}$
be unital
![]() $C^*$
-algebras, let
$C^*$
-algebras, let
![]() $\varPhi \colon \mathcal {A} \rightarrow \mathcal {B}$
be a unital positive linear map, let
$\varPhi \colon \mathcal {A} \rightarrow \mathcal {B}$
be a unital positive linear map, let
![]() $a\in \mathcal {A}$
be self-adjoint, and let
$a\in \mathcal {A}$
be self-adjoint, and let
![]() $p,q$
be positive integers such that
$p,q$
be positive integers such that
![]() $p<q$
,
$p<q$
,
![]() $p$
is odd, and
$p$
is odd, and
![]() $q$
is even. Then the following conditions are equivalent:
$q$
is even. Then the following conditions are equivalent:
-
(i)
 $\varPhi $
restricted to the unital subalgebra generated by
$\varPhi $
restricted to the unital subalgebra generated by
 $\{a\}$
is multiplicative.
$\{a\}$
is multiplicative. -
(ii) There exists a self-adjoint element
 $b\in \mathcal {B}$
such that
$b\in \mathcal {B}$
such that
 $b^k = \varPhi (a^k)$
, for
$b^k = \varPhi (a^k)$
, for
 $k=p,q$
.
$k=p,q$
.
Moreover, if (ii) holds, then
![]() $b=\varPhi (a)$
.
$b=\varPhi (a)$
.
In the complementary result, we show that the set
where
![]() $\mathbb {N}=\{1,2,3, \ldots \}$
, is the largest possible subset of
$\mathbb {N}=\{1,2,3, \ldots \}$
, is the largest possible subset of
![]() $\{(p,q)\in \mathbb {N}^2\colon p \leqslant q\}$
for which Problem 1.4 has an affirmative solution for
$\{(p,q)\in \mathbb {N}^2\colon p \leqslant q\}$
for which Problem 1.4 has an affirmative solution for
![]() $\varXi =\{p,q\}$
. Surprisingly, suitable counterexamples can be constructed even when the underlying Hilbert space
$\varXi =\{p,q\}$
. Surprisingly, suitable counterexamples can be constructed even when the underlying Hilbert space
![]() $\mathcal {H}$
is one-dimensional (see Theorem 5.2 for more details).
$\mathcal {H}$
is one-dimensional (see Theorem 5.2 for more details).
Theorem 1.9 Let
![]() $(p,q)\in \mathbb {N}^2\backslash \varOmega $
be such that
$(p,q)\in \mathbb {N}^2\backslash \varOmega $
be such that
![]() $p\leqslant q$
. Then there exist a Hilbert space
$p\leqslant q$
. Then there exist a Hilbert space
![]() $\mathcal {H}$
, a self-adjoint operator
$\mathcal {H}$
, a self-adjoint operator
![]() $T\in \boldsymbol {B}(\mathcal {H})$
, and a semispectral measure
$T\in \boldsymbol {B}(\mathcal {H})$
, and a semispectral measure
![]() $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
with compact support which is not spectral and such that
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
with compact support which is not spectral and such that
The proofs of Theorems 1.7–1.9 will be given in Sections 3–5, respectively. In Section 2, we provide the basic facts on operator monotone functions, positive linear maps on
![]() $C^*$
-algebras, and related operator inequalities needed in this paper. Section 6 contains additional counterexamples (including the case of infinite-dimensional spaces) related to the Fibonacci sequence. Finally, in Section 7, we discuss the possibility of adapting the two-moment characterizations of spectral measures given in Theorems 1.3 and 1.7 to the case of semispectral measures whose closed supports are not compact.
$C^*$
-algebras, and related operator inequalities needed in this paper. Section 6 contains additional counterexamples (including the case of infinite-dimensional spaces) related to the Fibonacci sequence. Finally, in Section 7, we discuss the possibility of adapting the two-moment characterizations of spectral measures given in Theorems 1.3 and 1.7 to the case of semispectral measures whose closed supports are not compact.
2 Prerequisites
In this paper, we use the following notation. The fields of real and complex numbers are denoted by
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $\mathbb {C}$
, respectively. The symbols
$\mathbb {C}$
, respectively. The symbols
![]() $\mathbb {N}$
,
$\mathbb {N}$
,
![]() $\mathbb {Z}_{+}$
, and
$\mathbb {Z}_{+}$
, and
![]() $\mathbb {R}_+$
stand for the sets of positive integers, nonnegative integers, and nonnegative real numbers, respectively. We write
$\mathbb {R}_+$
stand for the sets of positive integers, nonnegative integers, and nonnegative real numbers, respectively. We write
![]() $\mathfrak {B}(X)$
for the
$\mathfrak {B}(X)$
for the
![]() $\sigma $
-algebra of all Borel subsets of a topological Hausdorff space
$\sigma $
-algebra of all Borel subsets of a topological Hausdorff space
![]() $X$
. The
$X$
. The
![]() $C^*$
-algebra of all continuous complex functions on a compact Hausdorff space
$C^*$
-algebra of all continuous complex functions on a compact Hausdorff space
![]() $K$
equipped with supremum norm is denoted by
$K$
equipped with supremum norm is denoted by
![]() $C(K)$
. For
$C(K)$
. For
![]() $\lambda \in \mathbb {R}$
,
$\lambda \in \mathbb {R}$
,
![]() $\delta _{\lambda }$
stands for the Borel probability measure on
$\delta _{\lambda }$
stands for the Borel probability measure on
![]() $\mathbb {R}$
concentrated on
$\mathbb {R}$
concentrated on
![]() $\{\lambda \}$
.
$\{\lambda \}$
.
Let
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $\mathcal {K}$
be (complex) Hilbert spaces. Denote by
$\mathcal {K}$
be (complex) Hilbert spaces. Denote by
![]() $\boldsymbol {B}(\mathcal {H}, \mathcal {K})$
the Banach space of all bounded linear operators from
$\boldsymbol {B}(\mathcal {H}, \mathcal {K})$
the Banach space of all bounded linear operators from
![]() $\mathcal {H}$
to
$\mathcal {H}$
to
![]() $\mathcal {K}$
. If
$\mathcal {K}$
. If
![]() $A\in \boldsymbol {B}(\mathcal {H},\mathcal {K})$
, then
$A\in \boldsymbol {B}(\mathcal {H},\mathcal {K})$
, then
![]() $A^*$
,
$A^*$
,
![]() $\mathcal {N}(A)$
, and
$\mathcal {N}(A)$
, and
![]() $\mathcal {R}(A)$
stand for the adjoint, the kernel, and the range of
$\mathcal {R}(A)$
stand for the adjoint, the kernel, and the range of
![]() $A$
, respectively. It is well known that
$A$
, respectively. It is well known that
![]() $\boldsymbol {B}(\mathcal {H}):=\boldsymbol {B}(\mathcal {H},\mathcal {H})$
is a
$\boldsymbol {B}(\mathcal {H}):=\boldsymbol {B}(\mathcal {H},\mathcal {H})$
is a
![]() $C^*$
-algebra with unit
$C^*$
-algebra with unit
![]() $I$
, where
$I$
, where
![]() $I=I_{\mathcal {H}}$
denotes the identity operator on
$I=I_{\mathcal {H}}$
denotes the identity operator on
![]() $\mathcal {H}$
. We say that
$\mathcal {H}$
. We say that
![]() $A\in \boldsymbol {B}(\mathcal {H})$
is self-adjoint if
$A\in \boldsymbol {B}(\mathcal {H})$
is self-adjoint if
![]() $A=A^*$
, positive if
$A=A^*$
, positive if
![]() $\langle Ah,h\rangle \geqslant 0$
for all
$\langle Ah,h\rangle \geqslant 0$
for all
![]() $h\in \mathcal {H}$
, and an orthogonal projection if
$h\in \mathcal {H}$
, and an orthogonal projection if
![]() $A=A^*$
and
$A=A^*$
and
![]() $A=A^2$
.
$A=A^2$
.
Let
![]() $\mathscr {A}$
be a
$\mathscr {A}$
be a
![]() $\sigma $
-algebra of subsets of a set
$\sigma $
-algebra of subsets of a set
![]() $X$
, and let
$X$
, and let
![]() $F\colon \mathscr {A} \to \boldsymbol {B}(\mathcal {H})$
be a semispectral measure. Denote by
$F\colon \mathscr {A} \to \boldsymbol {B}(\mathcal {H})$
be a semispectral measure. Denote by
![]() $L^1(F)$
the vector space of all
$L^1(F)$
the vector space of all
![]() $\mathscr {A}$
-measurable functions
$\mathscr {A}$
-measurable functions
![]() $f\colon X \to \mathbb {C}$
such that
$f\colon X \to \mathbb {C}$
such that
![]() $\int _{X} |f(x)| \langle F(\mathrm {d\hspace {.1ex}} x)h, h\rangle < \infty $
for all
$\int _{X} |f(x)| \langle F(\mathrm {d\hspace {.1ex}} x)h, h\rangle < \infty $
for all
![]() $h\in \mathcal {H}$
. Then, for every
$h\in \mathcal {H}$
. Then, for every
![]() $f\in L^1(F)$
, there exists a unique operator
$f\in L^1(F)$
, there exists a unique operator
![]() $\int _X f \mathrm {d\hspace {.1ex}} F \in \boldsymbol {B}(\mathcal {H})$
such that (see, e.g., [Reference Stochel51, Appendix])
$\int _X f \mathrm {d\hspace {.1ex}} F \in \boldsymbol {B}(\mathcal {H})$
such that (see, e.g., [Reference Stochel51, Appendix])
If
![]() $F$
is a spectral measure, then
$F$
is a spectral measure, then
![]() $\int _X f \mathrm {d\hspace {.1ex}} F$
coincides with the usual spectral integral. In particular, if
$\int _X f \mathrm {d\hspace {.1ex}} F$
coincides with the usual spectral integral. In particular, if
![]() $F$
is the spectral measure of a self-adjoint operator
$F$
is the spectral measure of a self-adjoint operator
![]() $A\in \boldsymbol {B}(\mathcal {H})$
, then we write
$A\in \boldsymbol {B}(\mathcal {H})$
, then we write
![]() $f(A)=\int _{\mathbb {R}} f \mathrm {d\hspace {.1ex}} F$
for any
$f(A)=\int _{\mathbb {R}} f \mathrm {d\hspace {.1ex}} F$
for any
![]() $F$
-essentially bounded Borel function
$F$
-essentially bounded Borel function
![]() $f\colon \mathbb {R} \to \mathbb {R}$
; the map
$f\colon \mathbb {R} \to \mathbb {R}$
; the map
![]() $f \mapsto f(A)$
is called the Stone–von Neumann functional calculus. For more information needed in this article on spectral integrals, including the spectral theorem for self-adjoint operators and the Stone–von Neumann functional calculus, we refer the reader to [Reference Rudin46, Reference Schmüdgen48, Reference Weidmann54].
$f \mapsto f(A)$
is called the Stone–von Neumann functional calculus. For more information needed in this article on spectral integrals, including the spectral theorem for self-adjoint operators and the Stone–von Neumann functional calculus, we refer the reader to [Reference Rudin46, Reference Schmüdgen48, Reference Weidmann54].
Let
![]() $J\subseteq \mathbb {R}$
be an interval (which may be open, half-open, or closed; bounded or unbounded). A continuous function
$J\subseteq \mathbb {R}$
be an interval (which may be open, half-open, or closed; bounded or unbounded). A continuous function
![]() $f \colon J \rightarrow \mathbb {R}$
is said to be operator monotone if
$f \colon J \rightarrow \mathbb {R}$
is said to be operator monotone if
![]() $f(A)\leqslant f(B)$
for any two self-adjoint operators
$f(A)\leqslant f(B)$
for any two self-adjoint operators
![]() $A,B\in \boldsymbol {B}(\mathcal {H})$
such that
$A,B\in \boldsymbol {B}(\mathcal {H})$
such that
![]() $A\leqslant B$
and the spectra of
$A\leqslant B$
and the spectra of
![]() $A$
and
$A$
and
![]() $B$
are contained in
$B$
are contained in
![]() $J$
. In [Reference Löwner33], Löwner proved that a continuous function defined on an open interval is operator monotone if and only if it has an analytic continuation to the complex upper half-plane which is a Pick function (see also [Reference Donoghue18, Reference Hansen21]). Operator monotone functions have integral representations with respect to suitable positive Borel measures. In particular, a continuous function
$J$
. In [Reference Löwner33], Löwner proved that a continuous function defined on an open interval is operator monotone if and only if it has an analytic continuation to the complex upper half-plane which is a Pick function (see also [Reference Donoghue18, Reference Hansen21]). Operator monotone functions have integral representations with respect to suitable positive Borel measures. In particular, a continuous function
![]() $f \colon (0, \infty ) \rightarrow \mathbb {R}$
is operator monotone if and only if there exists a positive Borel measure
$f \colon (0, \infty ) \rightarrow \mathbb {R}$
is operator monotone if and only if there exists a positive Borel measure
![]() $\nu $
on
$\nu $
on
![]() $[0,\infty )$
such that
$[0,\infty )$
such that
![]() $\int _0^{\infty } \frac {1}{1+\lambda ^2}\mathrm {d\hspace {.1ex}} \nu (\lambda )<\infty $
and
$\int _0^{\infty } \frac {1}{1+\lambda ^2}\mathrm {d\hspace {.1ex}} \nu (\lambda )<\infty $
and
where
![]() $\alpha \in \mathbb {R}$
and
$\alpha \in \mathbb {R}$
and
![]() $\beta \in \mathbb {R}_+$
(see [Reference Hansen21, Theorem 5.2] or [Reference Bhatia9, p. 144]). The most important example of an operator monotone function is
$\beta \in \mathbb {R}_+$
(see [Reference Hansen21, Theorem 5.2] or [Reference Bhatia9, p. 144]). The most important example of an operator monotone function is
![]() $f\colon [0,\infty )\ni t\rightarrow t^p\in \mathbb {R}$
, where
$f\colon [0,\infty )\ni t\rightarrow t^p\in \mathbb {R}$
, where
![]() $p\in (0,1)$
. This function has the following integral representation (see [Reference Bhatia9, Exercise V.1.10(iii)] or [Reference Bhatia9, Exercise V.4.20]):
$p\in (0,1)$
. This function has the following integral representation (see [Reference Bhatia9, Exercise V.1.10(iii)] or [Reference Bhatia9, Exercise V.4.20]):
Operator monotone functions are related to the Hansen inequality [Reference Hansen20]. In [Reference Uchiyama52, Lemma 2.2], Uchiyama gave a necessary and sufficient condition for equality to hold in the Hansen inequality when the external factor is a nontrivial orthogonal projection (see the “moreover” part of Theorem 2.1; see also the paragraph before [Reference Pietrzycki and Stochel43, Theorem 2.4] showing why the separability of
![]() $\mathcal {H}$
can be dropped).
$\mathcal {H}$
can be dropped).
Theorem 2.1 [Reference Hansen20, Reference Uchiyama52]
Let
![]() $A\in \boldsymbol {B}(\mathcal {H})$
be a positive operator, let
$A\in \boldsymbol {B}(\mathcal {H})$
be a positive operator, let
![]() $T \in \boldsymbol {B}(\mathcal {H})$
be a contraction, and let
$T \in \boldsymbol {B}(\mathcal {H})$
be a contraction, and let
![]() $f\colon [0,\infty )\rightarrow \mathbb {R}$
be a continuous operator monotone function such that
$f\colon [0,\infty )\rightarrow \mathbb {R}$
be a continuous operator monotone function such that
![]() $f(0)\geqslant 0$
. Then
$f(0)\geqslant 0$
. Then
Moreover, if
![]() $f$
is not an affine function and
$f$
is not an affine function and
![]() $T$
is an orthogonal projection such that
$T$
is an orthogonal projection such that
![]() $T \neq I$
, then equality holds in (2.3) if and only if
$T \neq I$
, then equality holds in (2.3) if and only if
![]() $TA=AT$
and
$TA=AT$
and
![]() $f(0)=0$
.
$f(0)=0$
.
The reader is referred to [Reference Bhatia9, Reference Donoghue18, Reference Hansen20, Reference Hansen21, Reference Löwner33, Reference Simon49] for the fundamentals of the theory of operator monotone functions.
A linear map
![]() $\varPhi \colon \mathcal {A} \rightarrow \mathcal { B}$
between unital
$\varPhi \colon \mathcal {A} \rightarrow \mathcal { B}$
between unital
![]() $C^*$
-algebras is said to be positive if
$C^*$
-algebras is said to be positive if
![]() $\varPhi (a) \geqslant 0$
for every
$\varPhi (a) \geqslant 0$
for every
![]() $a\in \mathcal {A}$
such that
$a\in \mathcal {A}$
such that
![]() $a \geqslant 0$
. The map
$a \geqslant 0$
. The map
![]() $\varPhi $
is called unital if it preserves the units. If
$\varPhi $
is called unital if it preserves the units. If
![]() $\varPhi $
is positive and unital, then the following inequality, called Kadison’s inequality (see [Reference Kadison27, Theorem 1]), holds:
$\varPhi $
is positive and unital, then the following inequality, called Kadison’s inequality (see [Reference Kadison27, Theorem 1]), holds:
In this paper, we will need the Lieb–Ruskai inequality, which can be thought of as a Kadison-type inequality.
Theorem 2.2 [Reference Lieb and Ruskai32, Theorem 2]
Let
![]() $R\in \boldsymbol {B}(\mathcal {H},\mathcal {K})$
, and let
$R\in \boldsymbol {B}(\mathcal {H},\mathcal {K})$
, and let
![]() $\varPhi \colon \boldsymbol {B}(\mathcal {K})\to \boldsymbol {B}(\mathcal {H})$
be the positive linear map defined by
$\varPhi \colon \boldsymbol {B}(\mathcal {K})\to \boldsymbol {B}(\mathcal {H})$
be the positive linear map defined by
Then, for all
![]() $A,B\in \boldsymbol {B}(\mathcal {K})$
, the net
$A,B\in \boldsymbol {B}(\mathcal {K})$
, the net
![]() $\{\varPhi (A^*B)(\varPhi (B^*B)+\varepsilon I)^{-1}\varPhi (B^*A)\}_{\varepsilon>0}$
is convergent in the strong operator topology as
$\{\varPhi (A^*B)(\varPhi (B^*B)+\varepsilon I)^{-1}\varPhi (B^*A)\}_{\varepsilon>0}$
is convergent in the strong operator topology as
![]() $\varepsilon \downarrow 0$
and
$\varepsilon \downarrow 0$
and
3 Proof of Theorem 1.7
We begin with the following lemma, which gives a necessary and sufficient condition for equality to hold in a Kadison-type inequality (cf. (2.4)). Although this is a known fact even for unbounded operators (see [Reference Kruszyński and de Muynck31, Lemmas 1 and 2]), we will provide a brief algebraic proof for the reader’s convenience. Note also that part (iii) of Lemma 3.1 is [Reference Fuglede19, Lemma in Section 6].
Lemma 3.1 Let
![]() $T\in \boldsymbol {B}(\mathcal {H})$
be a self-adjoint operator, and let
$T\in \boldsymbol {B}(\mathcal {H})$
be a self-adjoint operator, and let
![]() $P \in \boldsymbol {B}(\mathcal {H})$
be an orthogonal projection. Then the following statements are valid:
$P \in \boldsymbol {B}(\mathcal {H})$
be an orthogonal projection. Then the following statements are valid:
-
(i)
 $(PTP)^2 \leqslant PT^{2}P$
.
$(PTP)^2 \leqslant PT^{2}P$
. -
(ii) Equality holds in (i) if and only if
 $PT=TP$
.
$PT=TP$
. -
(iii) If
 $T$
is an orthogonal projection, then
$T$
is an orthogonal projection, then
 $PTP$
is an orthogonal projection if and only if
$PTP$
is an orthogonal projection if and only if
 $PT=TP$
.
$PT=TP$
.
Proof (i) This is a direct consequence of the following algebraic identities:
 $$ \begin{align} \notag PT^{2}P-(PTP)^2 & = PT^{2}P- PTPTP \\ \notag & = PT(I-P)TP \\ & = (TP)^*(I-P)TP \geqslant 0. \end{align} $$
$$ \begin{align} \notag PT^{2}P-(PTP)^2 & = PT^{2}P- PTPTP \\ \notag & = PT(I-P)TP \\ & = (TP)^*(I-P)TP \geqslant 0. \end{align} $$
(ii) It follows from (3.1) that equality holds in (i) if and only if
or equivalently if and only if
which in turn is equivalent to
![]() $(I-P)TP=0$
. The last equality holds if and only if
$(I-P)TP=0$
. The last equality holds if and only if
![]() $TP=PTP$
, which by
$TP=PTP$
, which by
![]() $(PTP)^*=PTP$
is equivalent to
$(PTP)^*=PTP$
is equivalent to
![]() $PT=TP$
.
$PT=TP$
.
(iii) This is a direct consequence of (ii) because
![]() $PTP$
is an orthogonal projection if and only if
$PTP$
is an orthogonal projection if and only if
![]() $(PTP)^2 = PT^2P$
.
$(PTP)^2 = PT^2P$
.
For our further considerations, the following fact is fundamental. In particular, in view of Naimark’s dilation theorem (see the Introduction), it shows that Problems 1.4 and 1.5 are logically equivalent.
Lemma 3.2 Let
![]() $\mathcal {H}$
,
$\mathcal {H}$
,
![]() $\mathcal {K}$
be Hilbert spaces such that
$\mathcal {K}$
be Hilbert spaces such that
![]() $\mathcal {H}\subseteq \mathcal {K}$
and
$\mathcal {H}\subseteq \mathcal {K}$
and
![]() $P\in \boldsymbol {B}(\mathcal {K})$
be the orthogonal projection of
$P\in \boldsymbol {B}(\mathcal {K})$
be the orthogonal projection of
![]() $\mathcal {K}$
onto
$\mathcal {K}$
onto
![]() $\mathcal {H}$
. Suppose that
$\mathcal {H}$
. Suppose that
![]() $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
is a semispectral measure and
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
is a semispectral measure and
![]() $E\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {K})$
is a spectral measure such that
$E\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {K})$
is a spectral measure such that
SetFootnote
4
![]() $S:=\int _{\mathbb {R}} x E(\mathrm {d\hspace {.1ex}} x)$
. Then the following statements are valid:
$S:=\int _{\mathbb {R}} x E(\mathrm {d\hspace {.1ex}} x)$
. Then the following statements are valid:
-
(i)
 $F$
is spectral if and only if
$F$
is spectral if and only if
 $P$
commutes with
$P$
commutes with
 $E$
(equivalently,
$E$
(equivalently,
 $\mathcal {H}$
reduces
$\mathcal {H}$
reduces
 $E$
).
$E$
). -
(ii) If
 $S\in \boldsymbol {B}(\mathcal {K})$
, then
$S\in \boldsymbol {B}(\mathcal {K})$
, then
 $F$
has compact support and (3.3)
$F$
has compact support and (3.3) $$ \begin{align} P S^k|_{\mathcal{H}}=\int_{\mathbb{R}} x^k F(\mathrm{d\hspace{.1ex}} x), \quad k\in \mathbb{Z}_+. \end{align} $$
$$ \begin{align} P S^k|_{\mathcal{H}}=\int_{\mathbb{R}} x^k F(\mathrm{d\hspace{.1ex}} x), \quad k\in \mathbb{Z}_+. \end{align} $$
-
(iii) If
 $F$
has compact support and
$F$
has compact support and
 $\mathcal {K}$
is minimal, that is, (3.4)then
$\mathcal {K}$
is minimal, that is, (3.4)then $$ \begin{align} \mathcal{K} = \bigvee\{E(\varDelta)\mathcal{H} \colon \varDelta \in \mathfrak{B}(\mathbb{R})\}, \end{align} $$
$$ \begin{align} \mathcal{K} = \bigvee\{E(\varDelta)\mathcal{H} \colon \varDelta \in \mathfrak{B}(\mathbb{R})\}, \end{align} $$
 $E$
has compact support,
$E$
has compact support,
 $S\in \boldsymbol {B}(\mathcal {K})$
, and
$S\in \boldsymbol {B}(\mathcal {K})$
, and
 $S=S^*$
.
$S=S^*$
.
Proof (i) Set
![]() $\hat {F}(\varDelta ) = F(\varDelta )\oplus 0$
for
$\hat {F}(\varDelta ) = F(\varDelta )\oplus 0$
for
![]() $\varDelta \in \mathfrak {B}(\mathbb {R})$
, where
$\varDelta \in \mathfrak {B}(\mathbb {R})$
, where
![]() $0$
stands for the zero operator on
$0$
stands for the zero operator on
![]() $\mathcal {K} \ominus \mathcal {H}$
. Then, by (3.2),
$\mathcal {K} \ominus \mathcal {H}$
. Then, by (3.2),
![]() $\hat {F}(\varDelta ) = PE(\varDelta )P$
. Hence, observing that
$\hat {F}(\varDelta ) = PE(\varDelta )P$
. Hence, observing that
![]() $F(\varDelta )$
is an orthogonal projection if and only if
$F(\varDelta )$
is an orthogonal projection if and only if
![]() $\hat {F}(\varDelta )$
is an orthogonal projection and using Lemma 3.1(iii), we obtain (i).
$\hat {F}(\varDelta )$
is an orthogonal projection and using Lemma 3.1(iii), we obtain (i).
(ii) It follows from (3.2) that the closed support of
![]() $F$
is contained in the closed support of
$F$
is contained in the closed support of
![]() $E$
. Since
$E$
. Since
![]() $E$
has compact support (because
$E$
has compact support (because
![]() $S\in \boldsymbol {B}(\mathcal {K})$
; see [Reference Schmüdgen48, Theorem 5.9]), so does
$S\in \boldsymbol {B}(\mathcal {K})$
; see [Reference Schmüdgen48, Theorem 5.9]), so does
![]() $F$
. Applying the Stone–von Neumann functional calculus, we get
$F$
. Applying the Stone–von Neumann functional calculus, we get
 $$ \begin{align*} \langle P S^k|_{\mathcal{H}} h, h \rangle = \langle S^k h, h \rangle & = \int_{\mathbb{R}} x^k \langle E(\mathrm{d\hspace{.1ex}} x)h,h\rangle \\ & \hspace{-1ex}\overset{(3.2)}= \int_{\mathbb{R}} x^k \langle F(\mathrm{d\hspace{.1ex}} x)h,h\rangle \\ & \hspace{-1ex}\overset{(2.1)}= \Big\langle \int_{\mathbb{R}} x^k F(\mathrm{d\hspace{.1ex}} x)h,h\Big\rangle, \quad h \in \mathcal{H}, \, k \in \mathbb{Z}_+, \end{align*} $$
$$ \begin{align*} \langle P S^k|_{\mathcal{H}} h, h \rangle = \langle S^k h, h \rangle & = \int_{\mathbb{R}} x^k \langle E(\mathrm{d\hspace{.1ex}} x)h,h\rangle \\ & \hspace{-1ex}\overset{(3.2)}= \int_{\mathbb{R}} x^k \langle F(\mathrm{d\hspace{.1ex}} x)h,h\rangle \\ & \hspace{-1ex}\overset{(2.1)}= \Big\langle \int_{\mathbb{R}} x^k F(\mathrm{d\hspace{.1ex}} x)h,h\Big\rangle, \quad h \in \mathcal{H}, \, k \in \mathbb{Z}_+, \end{align*} $$
which implies (3.3).
(iii) By (3.2) and (3.4), the closed supports of the POV measures
![]() $E$
and
$E$
and
![]() $F$
coincide (see the proofs of [Reference Jabłoński24, Theorem 4.4] and [Reference Jung and Stochel26, Proposition 4(iii)]). Hence, the closed support of
$F$
coincide (see the proofs of [Reference Jabłoński24, Theorem 4.4] and [Reference Jung and Stochel26, Proposition 4(iii)]). Hence, the closed support of
![]() $E$
is compact. As a consequence, the operator
$E$
is compact. As a consequence, the operator
![]() $\int _{\mathbb {R}} x E(\mathrm {d\hspace {.1ex}} x)$
is bounded and self-adjoint (see [Reference Schmüdgen48, Theorem 5.9]). This completes the proof.
$\int _{\mathbb {R}} x E(\mathrm {d\hspace {.1ex}} x)$
is bounded and self-adjoint (see [Reference Schmüdgen48, Theorem 5.9]). This completes the proof.
We are now in a position to prove the main result of this paper, which provides a two-moment characterization of spectral measures.
Proof of Theorem 1.7 (i)
![]() $\Rightarrow $
(ii) This is immediate from the Stone–von Neumann functional calculus.
$\Rightarrow $
(ii) This is immediate from the Stone–von Neumann functional calculus.
(ii)
![]() $\Rightarrow $
(iii) Obvious.
$\Rightarrow $
(iii) Obvious.
(iii)
![]() $\Rightarrow $
(i) It follows from Naimark’s dilation theorem (see the Introduction) that there exist a Hilbert space
$\Rightarrow $
(i) It follows from Naimark’s dilation theorem (see the Introduction) that there exist a Hilbert space
![]() $\mathcal {K}$
containing
$\mathcal {K}$
containing
![]() $\mathcal {H}$
and a spectral measure
$\mathcal {H}$
and a spectral measure
![]() $E\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {K})$
such that (3.2) and (3.4) hold, where
$E\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {K})$
such that (3.2) and (3.4) hold, where
![]() $P\in \boldsymbol {B}(\mathcal {K})$
is the orthogonal projection of
$P\in \boldsymbol {B}(\mathcal {K})$
is the orthogonal projection of
![]() $\mathcal {K}$
onto
$\mathcal {K}$
onto
![]() $\mathcal {H}$
. By Lemma 3.2,
$\mathcal {H}$
. By Lemma 3.2,
![]() $E$
has compact support, the operator
$E$
has compact support, the operator
![]() $S:=\int _{\mathbb {R}} x E(\mathrm {d\hspace {.1ex}} x)$
is bounded and self-adjoint, and the following equalities are satisfied:
$S:=\int _{\mathbb {R}} x E(\mathrm {d\hspace {.1ex}} x)$
is bounded and self-adjoint, and the following equalities are satisfied:
First, we prove that
![]() $F$
is a spectral measure. In view of Lemma 3.2(i), it suffices to show that
$F$
is a spectral measure. In view of Lemma 3.2(i), it suffices to show that
![]() $P$
commutes with
$P$
commutes with
![]() $E$
. For this, we consider two cases.
$E$
. For this, we consider two cases.
Case 1.
![]() $p\leqslant \ \frac {q}{2}$
.
$p\leqslant \ \frac {q}{2}$
.
Let
![]() $\hat {T} \in \boldsymbol {B}(\mathcal {K})$
be defined by
$\hat {T} \in \boldsymbol {B}(\mathcal {K})$
be defined by
![]() $\hat {T} = T \oplus 0$
, where
$\hat {T} = T \oplus 0$
, where
![]() $0$
stands for the zero operator on
$0$
stands for the zero operator on
![]() $\mathcal {K} \ominus \mathcal {H}$
. Set
$\mathcal {K} \ominus \mathcal {H}$
. Set
![]() $q^{\prime }=\frac {q}{2}$
. Using Lemma 3.1(i) and then applying Theorem 2.1 to the positive operator
$q^{\prime }=\frac {q}{2}$
. Using Lemma 3.1(i) and then applying Theorem 2.1 to the positive operator
![]() $S^{2q^{\prime }}$
and the operator monotone function
$S^{2q^{\prime }}$
and the operator monotone function
![]() $f(t)=t^{\frac {p}{q^{\prime }}}$
(see (2.2)), we deduce that
$f(t)=t^{\frac {p}{q^{\prime }}}$
(see (2.2)), we deduce that
 $$ \begin{align*} \hat{T}^{2p} = (\hat{T}^{p})^2 & \overset{(3.5)} = (PS^{p}P)^2 \\ & \hspace{.9ex} \leqslant PS^{2p}P \\ & \hspace{.9ex} \leqslant (PS^{2q^{\prime}}P)^{\frac{p}{q^{\prime}}} = (PS^{q}P)^{\frac{2p}{q}} \overset{(3.5)} = (\hat{T}^q)^{\frac{2p}{q}} \overset{(*)}= \hat{T}^{2p}, \end{align*} $$
$$ \begin{align*} \hat{T}^{2p} = (\hat{T}^{p})^2 & \overset{(3.5)} = (PS^{p}P)^2 \\ & \hspace{.9ex} \leqslant PS^{2p}P \\ & \hspace{.9ex} \leqslant (PS^{2q^{\prime}}P)^{\frac{p}{q^{\prime}}} = (PS^{q}P)^{\frac{2p}{q}} \overset{(3.5)} = (\hat{T}^q)^{\frac{2p}{q}} \overset{(*)}= \hat{T}^{2p}, \end{align*} $$
where
![]() $(*)$
can be inferred from the hypothesis that
$(*)$
can be inferred from the hypothesis that
![]() $q$
is even. This implies that
$q$
is even. This implies that
It follows from Lemma 3.1(ii) that
Hence, by [Reference Schmüdgen48, Theorem 5.1],
![]() $P$
commutes with
$P$
commutes with
![]() $E_{p}$
, the spectral measure of
$E_{p}$
, the spectral measure of
![]() $S^{p}$
. By [Reference Birman and Solomjak10, Theorem 6.6.4],
$S^{p}$
. By [Reference Birman and Solomjak10, Theorem 6.6.4],
![]() $E_{p}$
is of the form
$E_{p}$
is of the form
where
![]() $\varphi _p\colon \mathbb {R} \to \mathbb {R}$
is a function given by
$\varphi _p\colon \mathbb {R} \to \mathbb {R}$
is a function given by
Since the map
![]() $\mathfrak {B}(\mathbb {R}) \ni \varDelta \mapsto \varphi _p^{-1}(\varDelta ) \in \mathfrak {B}(\mathbb {R})$
is surjective (because
$\mathfrak {B}(\mathbb {R}) \ni \varDelta \mapsto \varphi _p^{-1}(\varDelta ) \in \mathfrak {B}(\mathbb {R})$
is surjective (because
![]() $p$
is odd), we deduce from (3.6) that
$p$
is odd), we deduce from (3.6) that
![]() $P$
commutes with
$P$
commutes with
![]() $E$
.
$E$
.
Case 2.
![]() $p> \frac {q}{2}$
.
$p> \frac {q}{2}$
.
Without loss of generality, we can assume that
![]() $P\neq I_{\mathcal {K}}$
. Set
$P\neq I_{\mathcal {K}}$
. Set
![]() $q^{\prime }=\frac {q}{2}$
and
$q^{\prime }=\frac {q}{2}$
and
![]() $r=p-q^{\prime }$
. Since
$r=p-q^{\prime }$
. Since
![]() $p<q$
and
$p<q$
and
![]() $q$
is even, we see that
$q$
is even, we see that
![]() $r, q^{\prime } \in \mathbb {N}$
and
$r, q^{\prime } \in \mathbb {N}$
and
![]() $0 < \frac {r}{q^{\prime }}<1$
. By Theorem 2.1 applied to the positive operator
$0 < \frac {r}{q^{\prime }}<1$
. By Theorem 2.1 applied to the positive operator
![]() $S^{2q^{\prime }}$
and the operator monotone function
$S^{2q^{\prime }}$
and the operator monotone function
![]() $f(t)=t^{\frac {r}{q^{\prime }}}$
, we get
$f(t)=t^{\frac {r}{q^{\prime }}}$
, we get
This implies that
Let
![]() $\varPhi \colon \boldsymbol {B}(\mathcal {K})\to \boldsymbol {B}(\mathcal {H})$
be the positive unital linear map defined by
$\varPhi \colon \boldsymbol {B}(\mathcal {K})\to \boldsymbol {B}(\mathcal {H})$
be the positive unital linear map defined by
Applying Theorem 2.2 to
![]() $A=S^r$
,
$A=S^r$
,
![]() $B=S^{q^{\prime }}$
, and
$B=S^{q^{\prime }}$
, and
![]() $R\in \boldsymbol {B}(\mathcal {H},\mathcal {K})$
defined by
$R\in \boldsymbol {B}(\mathcal {H},\mathcal {K})$
defined by
![]() $Rh=h$
for
$Rh=h$
for
![]() $h\in \mathcal {H}$
leads to
$h\in \mathcal {H}$
leads to
Let
![]() $G\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
be the spectral measure of
$G\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
be the spectral measure of
![]() $T$
. Using the Stone–von Neumann functional calculus, we obtain
$T$
. Using the Stone–von Neumann functional calculus, we obtain
 $$ \begin{align} \notag \varPhi(S^{p})(\varPhi(S^{q})+\varepsilon I)^{-1}\varPhi(S^{p}) & \overset{(3.5)} = T^p(T^{q}+\varepsilon I)^{-1}T^p \\ & \hspace{1ex} =\int_{\mathbb{R}} \frac{x^{2p}}{x^{q}+\varepsilon}G(\mathrm{d\hspace{.1ex}} x), \quad \varepsilon \in (0,\infty). \end{align} $$
$$ \begin{align} \notag \varPhi(S^{p})(\varPhi(S^{q})+\varepsilon I)^{-1}\varPhi(S^{p}) & \overset{(3.5)} = T^p(T^{q}+\varepsilon I)^{-1}T^p \\ & \hspace{1ex} =\int_{\mathbb{R}} \frac{x^{2p}}{x^{q}+\varepsilon}G(\mathrm{d\hspace{.1ex}} x), \quad \varepsilon \in (0,\infty). \end{align} $$
Applying Lebesgue’s monotone convergence theorem and the hypothesis that
![]() $q$
is even and
$q$
is even and
![]() $2p-q\in \mathbb {N}$
, we deduce that
$2p-q\in \mathbb {N}$
, we deduce that
 $$ \begin{align*} \lim_{\varepsilon\downarrow 0} \langle\varPhi(S^{p}) (\varPhi(S^{q}) + \varepsilon I)^{-1} \varPhi(S^{p})h, h\rangle & \overset{(3.11)} = \lim_{\varepsilon\downarrow 0} \Big\langle\int_{\mathbb{R}} \frac{x^{2p}}{x^q+\varepsilon} G(\mathrm{d\hspace{.1ex}} x)h, h\Big\rangle \\ & \hspace{1.45ex}= \lim_{\varepsilon\downarrow 0} \int_{\mathbb{R}} \frac{x^{2p}}{x^q+\varepsilon}\langle G(\mathrm{d\hspace{.1ex}} x)h,h\rangle \\ & \hspace{1.45ex}=\int_{\mathbb{R}} {x^{2p-q}}\langle G(\mathrm{d\hspace{.1ex}} x)h, h\rangle \\ & \hspace{1.45ex} = \langle T^{2p-q}h,h\rangle \\ & \hspace{1.45ex} = \langle T^{2r}h,h\rangle, \quad h \in \mathcal{H}. \end{align*} $$
$$ \begin{align*} \lim_{\varepsilon\downarrow 0} \langle\varPhi(S^{p}) (\varPhi(S^{q}) + \varepsilon I)^{-1} \varPhi(S^{p})h, h\rangle & \overset{(3.11)} = \lim_{\varepsilon\downarrow 0} \Big\langle\int_{\mathbb{R}} \frac{x^{2p}}{x^q+\varepsilon} G(\mathrm{d\hspace{.1ex}} x)h, h\Big\rangle \\ & \hspace{1.45ex}= \lim_{\varepsilon\downarrow 0} \int_{\mathbb{R}} \frac{x^{2p}}{x^q+\varepsilon}\langle G(\mathrm{d\hspace{.1ex}} x)h,h\rangle \\ & \hspace{1.45ex}=\int_{\mathbb{R}} {x^{2p-q}}\langle G(\mathrm{d\hspace{.1ex}} x)h, h\rangle \\ & \hspace{1.45ex} = \langle T^{2p-q}h,h\rangle \\ & \hspace{1.45ex} = \langle T^{2r}h,h\rangle, \quad h \in \mathcal{H}. \end{align*} $$
Combined with (3.10), this implies that
Using (3.9) and (3.12), we get
This yields
or equivalently
which implies that equality holds in the Hansen inequality (3.8). Thus, by the moreover part of Theorem 2.1,
![]() $PS^{q}=S^{q}P$
(recall that
$PS^{q}=S^{q}P$
(recall that
![]() $q=2q^{\prime }$
). Hence,
$q=2q^{\prime }$
). Hence,
Therefore, we have
Take any
![]() $n_0\in \mathbb {N}$
such that
$n_0\in \mathbb {N}$
such that
![]() $p\leqslant \frac {q n_0}{2}$
. Then, by (3.5) and (3.13), we obtain
$p\leqslant \frac {q n_0}{2}$
. Then, by (3.5) and (3.13), we obtain
Since
![]() $p\leqslant \frac {q n_0}{2}$
, we can apply Case
$p\leqslant \frac {q n_0}{2}$
, we can apply Case
![]() $1$
to the pair
$1$
to the pair
![]() $(p,q n_0)$
in place of
$(p,q n_0)$
in place of
![]() $(p,q)$
. We then obtain that
$(p,q)$
. We then obtain that
![]() $P$
commutes with
$P$
commutes with
![]() $E$
.
$E$
.
Summarizing, we have proved that in both cases
![]() $F$
is a spectral measure. Therefore, to complete the proof, it remains to show that
$F$
is a spectral measure. Therefore, to complete the proof, it remains to show that
![]() $F$
is the spectral measure of
$F$
is the spectral measure of
![]() $T$
. Since
$T$
. Since
![]() $T^p = \int _{\mathbb {R}} x^p F(\mathrm {d\hspace {.1ex}} x)$
(by (iii)) and
$T^p = \int _{\mathbb {R}} x^p F(\mathrm {d\hspace {.1ex}} x)$
(by (iii)) and
![]() $T^p = \int _{\mathbb {R}} x^p G(\mathrm {d\hspace {.1ex}} x)$
(by Stone–von Neumann functional calculus), an application of [Reference Birman and Solomjak10, Theorem 6.6.4] shows that
$T^p = \int _{\mathbb {R}} x^p G(\mathrm {d\hspace {.1ex}} x)$
(by Stone–von Neumann functional calculus), an application of [Reference Birman and Solomjak10, Theorem 6.6.4] shows that
![]() $F\circ \varphi _{p}^{-1}$
and
$F\circ \varphi _{p}^{-1}$
and
![]() $G\circ \varphi _{p}^{-1}$
are spectral measures of
$G\circ \varphi _{p}^{-1}$
are spectral measures of
![]() $T^p$
, where
$T^p$
, where
![]() $G$
is the spectral measure of
$G$
is the spectral measure of
![]() $T$
,
$T$
,
![]() $\varphi _{p}$
is as in (3.7) and
$\varphi _{p}$
is as in (3.7) and
By the uniqueness part of [Reference Birman and Solomjak10, Theorem 6.1.1],
![]() $F\circ \varphi _p^{-1} = G\circ \varphi _p^{-1}$
. Since the map
$F\circ \varphi _p^{-1} = G\circ \varphi _p^{-1}$
. Since the map
![]() $\mathfrak {B}(\mathbb {R}) \ni \varDelta \mapsto \varphi _p^{-1}(\varDelta ) \in \mathfrak {B}(\mathbb {R})$
is surjective (because
$\mathfrak {B}(\mathbb {R}) \ni \varDelta \mapsto \varphi _p^{-1}(\varDelta ) \in \mathfrak {B}(\mathbb {R})$
is surjective (because
![]() $p$
is odd), we deduce that
$p$
is odd), we deduce that
![]() $F=G$
, so
$F=G$
, so
![]() $F$
is the spectral measure of
$F$
is the spectral measure of
![]() $T$
. This completes the proof.
$T$
. This completes the proof.
We conclude this section by providing some inequalities for operator moments of a semispectral measure on the real line. Although it is a well-known fact (see [Reference Bisgaard11] and the references therein), we outline its short proof for the reader’s convenience.
Proposition 3.3 Let
![]() $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
be a semispectral measure with compact support. Then
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
be a semispectral measure with compact support. Then
 $$ \begin{align*} \left[\begin{smallmatrix} I & \int_{\mathbb{R}} x F(\mathrm{d\hspace{.1ex}} x) & \cdots & \int_{\mathbb{R}} x^n F(\mathrm{d\hspace{.1ex}} x) \\[1ex] \int_{\mathbb{R}} x F(\mathrm{d\hspace{.1ex}} x) & \int_{\mathbb{R}} x^2 F(\mathrm{d\hspace{.1ex}} x) & \cdots & \int_{\mathbb{R}} x^{n+1} F(\mathrm{d\hspace{.1ex}} x) \\ \vdots & \vdots & \ddots & \vdots \\[1ex] \int_{\mathbb{R}} x^n F(\mathrm{d\hspace{.1ex}} x) & \int_{\mathbb{R}} x^{n+1} F(\mathrm{d\hspace{.1ex}} x) & \cdots & \int_{\mathbb{R}} x^{2n} F(\mathrm{d\hspace{.1ex}} x) \end{smallmatrix} \right] \geqslant 0,\quad n\in \mathbb{Z}_+. \end{align*} $$
$$ \begin{align*} \left[\begin{smallmatrix} I & \int_{\mathbb{R}} x F(\mathrm{d\hspace{.1ex}} x) & \cdots & \int_{\mathbb{R}} x^n F(\mathrm{d\hspace{.1ex}} x) \\[1ex] \int_{\mathbb{R}} x F(\mathrm{d\hspace{.1ex}} x) & \int_{\mathbb{R}} x^2 F(\mathrm{d\hspace{.1ex}} x) & \cdots & \int_{\mathbb{R}} x^{n+1} F(\mathrm{d\hspace{.1ex}} x) \\ \vdots & \vdots & \ddots & \vdots \\[1ex] \int_{\mathbb{R}} x^n F(\mathrm{d\hspace{.1ex}} x) & \int_{\mathbb{R}} x^{n+1} F(\mathrm{d\hspace{.1ex}} x) & \cdots & \int_{\mathbb{R}} x^{2n} F(\mathrm{d\hspace{.1ex}} x) \end{smallmatrix} \right] \geqslant 0,\quad n\in \mathbb{Z}_+. \end{align*} $$
Proof By Naimark’s dilation theorem (see the Introduction), there exist a Hilbert space
![]() $\mathcal {K}$
containing
$\mathcal {K}$
containing
![]() $\mathcal {H}$
and a spectral measure
$\mathcal {H}$
and a spectral measure
![]() $E\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {K})$
that satisfy (3.2) and (3.4). By Lemma 3.2(iii),
$E\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {K})$
that satisfy (3.2) and (3.4). By Lemma 3.2(iii),
![]() $E$
has compact support. Applying the Stone–von Neumann functional calculus, we obtain
$E$
has compact support. Applying the Stone–von Neumann functional calculus, we obtain
 $$ \begin{align*} \sum_{j,k=0}^n \Big\langle \int_{\mathbb{R}} x^{j+k} F(\mathrm{d\hspace{.1ex}} x) h_k, h_j\Big\rangle & =\sum_{j,k=0}^n \Big\langle \int_{\mathbb{R}} x^{j+k} E(\mathrm{d\hspace{.1ex}} x) h_k, h_j\Big\rangle \\ &= \Big\|\sum_{k=0}^n \int_{\mathbb{R}} x^k E(\mathrm{d\hspace{.1ex}} x) h_k\Big\|^2 \geqslant 0, \end{align*} $$
$$ \begin{align*} \sum_{j,k=0}^n \Big\langle \int_{\mathbb{R}} x^{j+k} F(\mathrm{d\hspace{.1ex}} x) h_k, h_j\Big\rangle & =\sum_{j,k=0}^n \Big\langle \int_{\mathbb{R}} x^{j+k} E(\mathrm{d\hspace{.1ex}} x) h_k, h_j\Big\rangle \\ &= \Big\|\sum_{k=0}^n \int_{\mathbb{R}} x^k E(\mathrm{d\hspace{.1ex}} x) h_k\Big\|^2 \geqslant 0, \end{align*} $$
for all finite sequences
![]() $\{h_k\}_{k=0}^n \subseteq \mathcal {H}$
.
$\{h_k\}_{k=0}^n \subseteq \mathcal {H}$
.
Corollary 3.4 Let
![]() $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
be a semispectral measure with compact support. Then
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
be a semispectral measure with compact support. Then
![]() $\mathrm {Var}(F) \geqslant 0$
, where
$\mathrm {Var}(F) \geqslant 0$
, where
![]() $\mathrm {Var}(F)$
is as in (1.2).
$\mathrm {Var}(F)$
is as in (1.2).
Proof Apply Proposition 3.3 with
![]() $n=1$
and use the following well-known fact (see [Reference Davis17, Lemma 1]; see also [Reference Moslehian, Kian and Xu35, Theorem 5.1]): if
$n=1$
and use the following well-known fact (see [Reference Davis17, Lemma 1]; see also [Reference Moslehian, Kian and Xu35, Theorem 5.1]): if
![]() $A, B \in \boldsymbol {B}(\mathcal {H})$
are self-adjoint,
$A, B \in \boldsymbol {B}(\mathcal {H})$
are self-adjoint,
![]() $A$
is invertible in
$A$
is invertible in
![]() $\boldsymbol {B}(\mathcal {H})$
and
$\boldsymbol {B}(\mathcal {H})$
and
![]() $X\in \boldsymbol {B}(\mathcal {H})$
, then
$X\in \boldsymbol {B}(\mathcal {H})$
, then
![]() $\left [\begin {smallmatrix} A & X \\ X^* & B \end {smallmatrix}\right ] \geqslant 0$
if and only if
$\left [\begin {smallmatrix} A & X \\ X^* & B \end {smallmatrix}\right ] \geqslant 0$
if and only if
![]() $B \geqslant X^*A^{-1}X$
.
$B \geqslant X^*A^{-1}X$
.
4 Proof of Theorem 1.8
We begin by stating a lemma needed in the proof of Theorem 1.8, which seems to be a folklore-type result. For the convenience of the reader, we provide its proof.
Lemma 4.1 Let
![]() $\mathcal {A}$
be a unital
$\mathcal {A}$
be a unital
![]() $C^*$
-algebra, let
$C^*$
-algebra, let
![]() $\varPhi \colon \mathcal {A} \to \boldsymbol {B}(\mathcal {H})$
be a unital positive linear map, and let
$\varPhi \colon \mathcal {A} \to \boldsymbol {B}(\mathcal {H})$
be a unital positive linear map, and let
![]() $a$
be a self-adjoint element of
$a$
be a self-adjoint element of
![]() $\mathcal {A}$
. Then there exists a unique semispectral measure
$\mathcal {A}$
. Then there exists a unique semispectral measure
![]() $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
such that
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
such that
![]() $x^n \in L^1(F)$
for all
$x^n \in L^1(F)$
for all
![]() $n\in \mathbb {Z}_+$
and
$n\in \mathbb {Z}_+$
and
Moreover,
![]() $F$
possesses the following properties:
$F$
possesses the following properties:
-
(i)
 $F$
has compact support.
$F$
has compact support. -
(ii) The closed support of
 $F$
is contained in
$F$
is contained in
 $\mathbb {R}_+$
whenever
$\mathbb {R}_+$
whenever
 $a\geqslant 0$
.
$a\geqslant 0$
.
First proof of Lemma 4.1
Replacing
![]() $\mathcal {A}$
by the unital
$\mathcal {A}$
by the unital
![]() $C^*$
-algebra generated by
$C^*$
-algebra generated by
![]() $\{a\}$
, we may assume without loss of generality that
$\{a\}$
, we may assume without loss of generality that
![]() $\mathcal {A}$
is commutative. According to [Reference Paulsen41, Corollary 2.9],
$\mathcal {A}$
is commutative. According to [Reference Paulsen41, Corollary 2.9],
![]() $\varPhi $
is contractive and therefore
$\varPhi $
is contractive and therefore
Since
![]() $a$
is self-adjoint, we see that
$a$
is self-adjoint, we see that
 $$ \begin{align*} \left[\begin{smallmatrix} e & a^1& \cdots & a^n \\[1ex] a^1 & a^2& \cdots & a^{n+1} \\ \vdots & \vdots & \ddots & \vdots \\[1ex] a^{n} & a^{n+1} & \cdots & a^{2n} \end{smallmatrix} \right] = \left[\begin{smallmatrix} e & a^1 & \cdots & a^n \\[1ex] 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\[1ex] 0 & 0 & \cdots & 0 \end{smallmatrix} \right]^* \left[\begin{smallmatrix} e & a^1 & \cdots & a^n \\[1ex] 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\[1ex] 0 & 0 & \cdots & 0 \end{smallmatrix} \right] \geqslant 0, \end{align*} $$
$$ \begin{align*} \left[\begin{smallmatrix} e & a^1& \cdots & a^n \\[1ex] a^1 & a^2& \cdots & a^{n+1} \\ \vdots & \vdots & \ddots & \vdots \\[1ex] a^{n} & a^{n+1} & \cdots & a^{2n} \end{smallmatrix} \right] = \left[\begin{smallmatrix} e & a^1 & \cdots & a^n \\[1ex] 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\[1ex] 0 & 0 & \cdots & 0 \end{smallmatrix} \right]^* \left[\begin{smallmatrix} e & a^1 & \cdots & a^n \\[1ex] 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\[1ex] 0 & 0 & \cdots & 0 \end{smallmatrix} \right] \geqslant 0, \end{align*} $$
where
![]() $e$
denotes the unit of
$e$
denotes the unit of
![]() $\mathcal {A}$
. By the Stinespring theorem (see [Reference Stinespring50, Theorem 4]),
$\mathcal {A}$
. By the Stinespring theorem (see [Reference Stinespring50, Theorem 4]),
![]() $\varPhi $
is completely positive, so
$\varPhi $
is completely positive, so
![]() $[\varPhi (a^{j+k})]_{j,k=0}^n\geqslant 0$
. In particular, we have
$[\varPhi (a^{j+k})]_{j,k=0}^n\geqslant 0$
. In particular, we have
 $$ \begin{align} \sum_{j,k=0}^n \bar \lambda_j \lambda_k \varPhi(a^{j+k}) \geqslant 0, \quad \{\lambda_j\}_{j=0}^n \subseteq \mathbb{C}, \, n \in \mathbb{Z}_+. \end{align} $$
$$ \begin{align} \sum_{j,k=0}^n \bar \lambda_j \lambda_k \varPhi(a^{j+k}) \geqslant 0, \quad \{\lambda_j\}_{j=0}^n \subseteq \mathbb{C}, \, n \in \mathbb{Z}_+. \end{align} $$
Using (4.1) and (4.2), we deduce from [Reference Bisgaard11, Theorem 2] that there exists a semispectral measure
![]() $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
such that
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
such that
(
![]() $F(\mathbb {R})=I$
because
$F(\mathbb {R})=I$
because
![]() $\varPhi $
is unital). Since
$\varPhi $
is unital). Since
![]() $\lim _{r\to \infty } \|f\|_r = \|f\|_{\infty }$
whenever
$\lim _{r\to \infty } \|f\|_r = \|f\|_{\infty }$
whenever
![]() $\|f\|_r < \infty $
for some
$\|f\|_r < \infty $
for some
![]() $r< \infty $
(see [Reference Rudin47, Exercise 4, p. 71]) and
$r< \infty $
(see [Reference Rudin47, Exercise 4, p. 71]) and
 $$ \begin{align*} \lim_{n\to \infty} \left(\int_{\mathbb{R}} x^{2n} \langle F(\mathrm{d\hspace{.1ex}} x)h,h\rangle\right)^{\frac{1}{2n}} \overset{(4.3)}= \lim_{n\to \infty} \langle\varPhi(a^{2n})h, h \rangle^{\frac{1}{2n}} \overset{(4.1)} \leqslant \|a\|, \quad h \in \mathcal{H}, \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty} \left(\int_{\mathbb{R}} x^{2n} \langle F(\mathrm{d\hspace{.1ex}} x)h,h\rangle\right)^{\frac{1}{2n}} \overset{(4.3)}= \lim_{n\to \infty} \langle\varPhi(a^{2n})h, h \rangle^{\frac{1}{2n}} \overset{(4.1)} \leqslant \|a\|, \quad h \in \mathcal{H}, \end{align*} $$
we deduce that
Thus, the closed support of
![]() $F$
is contained in
$F$
is contained in
![]() $[-\|a\|, \|a\|]$
. Combined with (2.1) and (4.3), this implies that
$[-\|a\|, \|a\|]$
. Combined with (2.1) and (4.3), this implies that
![]() $x^n \in L^1(F)$
for all
$x^n \in L^1(F)$
for all
![]() $n\in \mathbb {Z}_+$
and
$n\in \mathbb {Z}_+$
and
That
![]() $F$
is unique follows from (2.1) and the fact that a Hamburger moment sequence having a representing measure with compact support is determinate (see [Reference Fuglede19]).
$F$
is unique follows from (2.1) and the fact that a Hamburger moment sequence having a representing measure with compact support is determinate (see [Reference Fuglede19]).
Assume
![]() $a \geqslant 0$
. By the square root theorem (see [Reference Murphy36, Theorem 2.2.1]), we have
$a \geqslant 0$
. By the square root theorem (see [Reference Murphy36, Theorem 2.2.1]), we have
 $$ \begin{align*} \left[\begin{smallmatrix} a^1 & a^2 & \cdots & a^{n+1} \\[1ex] a^2 & a^3& \cdots & a^{n+2} \\ \vdots & \vdots & \ddots & \vdots \\[1ex] a^{n+1} & a^{n+2} & \cdots & a^{2n+1} \end{smallmatrix} \right] = \left[\begin{smallmatrix} a^{\frac{1}{2}} & a^{\frac{3}{2}} & \cdots & a^{\frac{2n+1}{2}} \\[1ex] 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\[1ex] 0 & 0 & \cdots & 0 \end{smallmatrix} \right]^* \left[\begin{smallmatrix} a^{\frac{1}{2}} & a^{\frac{3}{2}} & \cdots & a^{\frac{2n+1}{2}} \\[1ex] 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\[1ex] 0 & 0 & \cdots & 0 \end{smallmatrix} \right] \geqslant 0. \end{align*} $$
$$ \begin{align*} \left[\begin{smallmatrix} a^1 & a^2 & \cdots & a^{n+1} \\[1ex] a^2 & a^3& \cdots & a^{n+2} \\ \vdots & \vdots & \ddots & \vdots \\[1ex] a^{n+1} & a^{n+2} & \cdots & a^{2n+1} \end{smallmatrix} \right] = \left[\begin{smallmatrix} a^{\frac{1}{2}} & a^{\frac{3}{2}} & \cdots & a^{\frac{2n+1}{2}} \\[1ex] 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\[1ex] 0 & 0 & \cdots & 0 \end{smallmatrix} \right]^* \left[\begin{smallmatrix} a^{\frac{1}{2}} & a^{\frac{3}{2}} & \cdots & a^{\frac{2n+1}{2}} \\[1ex] 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\[1ex] 0 & 0 & \cdots & 0 \end{smallmatrix} \right] \geqslant 0. \end{align*} $$
Hence, by [Reference Stinespring50, Theorem 4],
![]() $[\varPhi (a^{j+k+1})]_{j,k=0}^n\geqslant 0$
, which implies that
$[\varPhi (a^{j+k+1})]_{j,k=0}^n\geqslant 0$
, which implies that
 $$ \begin{align} \sum_{j,k=0}^n \bar \lambda_j \lambda_k \varPhi(a^{j+k+1}) \geqslant 0, \quad \{\lambda_j\}_{j=0}^n \subseteq \mathbb{C}, \, n \in \mathbb{Z}_+. \end{align} $$
$$ \begin{align} \sum_{j,k=0}^n \bar \lambda_j \lambda_k \varPhi(a^{j+k+1}) \geqslant 0, \quad \{\lambda_j\}_{j=0}^n \subseteq \mathbb{C}, \, n \in \mathbb{Z}_+. \end{align} $$
Combining (4.2), (4.4), and the Stieltjes theorem [Reference Berg, Christensen and Ressel8, Theorem 6.2.5] with the fact that a Hamburger moment sequence having a representing measure with compact support is determinate, we see that the closed support of
![]() $F$
is contained in
$F$
is contained in
![]() $\mathbb {R}_+$
.
$\mathbb {R}_+$
.
Second proof of Lemma 4.1
As in the first proof, there is no loss of generality in assuming that
![]() $\mathcal {A}$
is commutative. Applying the Stinespring dilation theorem (see [Reference Stinespring50, Theorems 1 and 4]), we deduce that there exist a Hilbert space
$\mathcal {A}$
is commutative. Applying the Stinespring dilation theorem (see [Reference Stinespring50, Theorems 1 and 4]), we deduce that there exist a Hilbert space
![]() $\mathcal {K}$
containing
$\mathcal {K}$
containing
![]() $\mathcal {H}$
and a
$\mathcal {H}$
and a
![]() $*$
-representation
$*$
-representation
![]() $\pi \colon \mathcal {A}\to \boldsymbol {B}(\mathcal {K})$
such that
$\pi \colon \mathcal {A}\to \boldsymbol {B}(\mathcal {K})$
such that
where
![]() $P\in \boldsymbol {B}(\mathcal {K})$
is the orthogonal projection of
$P\in \boldsymbol {B}(\mathcal {K})$
is the orthogonal projection of
![]() $\mathcal {K}$
onto
$\mathcal {K}$
onto
![]() $\mathcal {H}$
. By [Reference Rudin46, Theorem 12.22], there exists a spectral measure
$\mathcal {H}$
. By [Reference Rudin46, Theorem 12.22], there exists a spectral measure
![]() $E\colon \mathfrak {B}(\mathfrak M) \to \boldsymbol {B}(\mathcal {K})$
such that
$E\colon \mathfrak {B}(\mathfrak M) \to \boldsymbol {B}(\mathcal {K})$
such that
where
![]() $\mathfrak {M}$
is the maximal ideal space of the unital commutative
$\mathfrak {M}$
is the maximal ideal space of the unital commutative
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\overline {\pi (\mathcal {A})}$
, the (operator norm) closure of
$\overline {\pi (\mathcal {A})}$
, the (operator norm) closure of
![]() $\pi (\mathcal {A})$
in
$\pi (\mathcal {A})$
in
![]() $\boldsymbol {B}(\mathcal {K})$
, and
$\boldsymbol {B}(\mathcal {K})$
, and
![]() $\widehat {\pi (u)}\colon \mathfrak {M} \to \mathbb {C}$
is the Gelfand transform of
$\widehat {\pi (u)}\colon \mathfrak {M} \to \mathbb {C}$
is the Gelfand transform of
![]() $\pi (u)$
. Set
$\pi (u)$
. Set
![]() $M =PE|_{\mathcal {H}}$
. It follows from (4.5) and (4.6) that
$M =PE|_{\mathcal {H}}$
. It follows from (4.5) and (4.6) that
By [Reference Rudin46, Theorem 11.18] and the assumption that
![]() $a=a^*$
, we see that
$a=a^*$
, we see that
![]() $\widehat {\pi (a)}(\mathfrak {M}) \subseteq \mathbb {R}$
. Define the semispectral measure
$\widehat {\pi (a)}(\mathfrak {M}) \subseteq \mathbb {R}$
. Define the semispectral measure
![]() $F \colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
by
$F \colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
by
Since
![]() $\widehat {\pi (a)}$
is continuous and
$\widehat {\pi (a)}$
is continuous and
![]() $\mathfrak {M}$
is a compact Hausdorff space, we deduce that
$\mathfrak {M}$
is a compact Hausdorff space, we deduce that
![]() $\widehat {\pi (a)}(\mathfrak {M})$
is a compact subset of
$\widehat {\pi (a)}(\mathfrak {M})$
is a compact subset of
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
![]() $F\big (\mathbb {R} \backslash \widehat {\pi (a)}(\mathfrak {M})\big )=0$
, which implies that
$F\big (\mathbb {R} \backslash \widehat {\pi (a)}(\mathfrak {M})\big )=0$
, which implies that
![]() $F$
has compact support. Applying (2.1) and the measure transport theorem (cf. [Reference Ash2, Theorem 1.6.12]), we conclude that
$F$
has compact support. Applying (2.1) and the measure transport theorem (cf. [Reference Ash2, Theorem 1.6.12]), we conclude that
The proof of the uniqueness of
![]() $F$
proceeds as before.
$F$
proceeds as before.
If
![]() $a\geqslant 0$
, then by the square root theorem and [Reference Rudin46, Theorem 11.18], we get
$a\geqslant 0$
, then by the square root theorem and [Reference Rudin46, Theorem 11.18], we get
which implies that the closed support of
![]() $F$
is contained in
$F$
is contained in
![]() $\mathbb {R}_+$
.
$\mathbb {R}_+$
.
Proof of Theorem 1.8 (i)
![]() $\Rightarrow $
(ii) Since the map
$\Rightarrow $
(ii) Since the map
![]() $\varPhi $
preserves self-adjointness,
$\varPhi $
preserves self-adjointness,
![]() $b:=\varPhi (a)$
does the job.
$b:=\varPhi (a)$
does the job.
(ii)
![]() $\Rightarrow $
(i) In view of the Gelfand–Naimark theorem (see [Reference Rudin46, Theorem 12.41]), there is no loss of generality in assuming that
$\Rightarrow $
(i) In view of the Gelfand–Naimark theorem (see [Reference Rudin46, Theorem 12.41]), there is no loss of generality in assuming that
![]() $\mathcal {B}=\boldsymbol {B}(\mathcal {H})$
. By Lemma 4.1, there exists a semispectral measure
$\mathcal {B}=\boldsymbol {B}(\mathcal {H})$
. By Lemma 4.1, there exists a semispectral measure
![]() $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
with compact support such that
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
with compact support such that
Therefore, by (ii), we have
Applying Theorem 1.7 to
![]() $T=b$
, we conclude that
$T=b$
, we conclude that
![]() $F$
is the spectral measure of
$F$
is the spectral measure of
![]() $b$
. Using the Stone–von Neumann functional calculus, we get
$b$
. Using the Stone–von Neumann functional calculus, we get
so
![]() $b=\varPhi (a)$
, which yields
$b=\varPhi (a)$
, which yields
![]() $\varPhi (a^n)=\varPhi (a)^n$
for all
$\varPhi (a^n)=\varPhi (a)^n$
for all
![]() $n\in \mathbb {Z}_+$
. This implies (i).
$n\in \mathbb {Z}_+$
. This implies (i).
Remark 4.2 We have deduced Theorem 1.8 from Theorem 1.7. It turns out that, conversely, Theorem 1.7 can be derived from Theorem 1.8. To do this, it suffices to show that under the assumptions and notation of Theorem 1.7, (iii) implies (i). So suppose that the condition (iii) of Theorem 1.7 holds. Define the unital positive linear map
![]() $\varPhi \colon C(K) \to \boldsymbol {B}(\mathcal {H})$
by
$\varPhi \colon C(K) \to \boldsymbol {B}(\mathcal {H})$
by
where
![]() $K$
stands for the closed support of
$K$
stands for the closed support of
![]() $F$
. Let
$F$
. Let
![]() $a\in C(K)$
be the function defined by
$a\in C(K)$
be the function defined by
![]() $a(x)=x$
for
$a(x)=x$
for
![]() $x\in K$
, and let
$x\in K$
, and let
![]() $b=T$
. Then
$b=T$
. Then
![]() $b^k = \varPhi (a^k)$
for
$b^k = \varPhi (a^k)$
for
![]() $k=p,q$
. Hence, by Theorem 1.8,
$k=p,q$
. Hence, by Theorem 1.8,
![]() $T=\int _{K} x F(\mathrm {d\hspace {.1ex}} x)$
and
$T=\int _{K} x F(\mathrm {d\hspace {.1ex}} x)$
and
where
![]() $G$
is the spectral measure of
$G$
is the spectral measure of
![]() $T$
. Using (2.1) and the fact that a Hamburger moment sequence having a representing measure with compact support is determinate, we conclude that
$T$
. Using (2.1) and the fact that a Hamburger moment sequence having a representing measure with compact support is determinate, we conclude that
![]() $F=G$
. This completes the proof.
$F=G$
. This completes the proof.
A careful inspection of the proof of Theorem 1.8 in conjunction with the above discussion shows that, in fact, Problems 1.4 and 1.6 are logically equivalent regardless of the cardinality of the set
![]() $\varXi $
.
$\varXi $
.
Remark 4.3 At first glance, it seems that Theorem 1.8 is related to a result of Petz (see [Reference Petz42, Theorem]), which shows that equality holds in Jensen’s inequality
![]() $f(\varPhi (a)) \leqslant \varPhi (f(a))$
if and only if
$f(\varPhi (a)) \leqslant \varPhi (f(a))$
if and only if
![]() $\varPhi $
restricted to the unital subalgebra generated by
$\varPhi $
restricted to the unital subalgebra generated by
![]() $\{a\}$
is multiplicative, where
$\{a\}$
is multiplicative, where
![]() $\varPhi $
is a unital positive linear map between unital
$\varPhi $
is a unital positive linear map between unital
![]() $C^*$
-algebras,
$C^*$
-algebras,
![]() $f$
is a non-affine operator convex function on an open subinterval
$f$
is a non-affine operator convex function on an open subinterval
![]() $J$
of
$J$
of
![]() $\mathbb {R}$
, and
$\mathbb {R}$
, and
![]() $a$
is a self-adjoint element with spectrum in
$a$
is a self-adjoint element with spectrum in
![]() $J$
. The main difference between Petz’s result and Theorem 1.8 is that the monomial
$J$
. The main difference between Petz’s result and Theorem 1.8 is that the monomial
![]() $x^n$
with
$x^n$
with
![]() $n\in \mathbb {Z}_+$
is a non-affine operator convex function on
$n\in \mathbb {Z}_+$
is a non-affine operator convex function on
![]() $J=\mathbb {R}$
if and only if
$J=\mathbb {R}$
if and only if
![]() $n = 2$
; this can be deduced from [Reference Bhatia9, Exercises V.1.3 and V.2.11] (cf. [Reference Rizvi and Shorrock45]). In the very special case of positive invertible elements, Petz’s theorem implies Theorem 1.8 (and Theorem 4.4) as shown in Remark 4.5. However, the authors see no way to deduce Theorem 1.8 from Petz’s theorem in the situation of general self-adjoint (or even positive noninvertible) elements. For this reason, the Lieb–Ruskai inequality turned out to be a key tool in the proof of Theorem 1.7, which in view of Remark 4.2 is equivalent to Theorem 1.8.
$n = 2$
; this can be deduced from [Reference Bhatia9, Exercises V.1.3 and V.2.11] (cf. [Reference Rizvi and Shorrock45]). In the very special case of positive invertible elements, Petz’s theorem implies Theorem 1.8 (and Theorem 4.4) as shown in Remark 4.5. However, the authors see no way to deduce Theorem 1.8 from Petz’s theorem in the situation of general self-adjoint (or even positive noninvertible) elements. For this reason, the Lieb–Ruskai inequality turned out to be a key tool in the proof of Theorem 1.7, which in view of Remark 4.2 is equivalent to Theorem 1.8.
In the case where the elements
![]() $a$
and
$a$
and
![]() $b$
are positive, we get the following version of Theorem 1.8.
$b$
are positive, we get the following version of Theorem 1.8.
Theorem 4.4 Suppose that
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal { B}$
are unital
$\mathcal { B}$
are unital
![]() $C^*$
-algebras,
$C^*$
-algebras,
![]() $\varPhi \colon \mathcal {A} \rightarrow \mathcal {B}$
is a unital positive linear map,
$\varPhi \colon \mathcal {A} \rightarrow \mathcal {B}$
is a unital positive linear map,
![]() $a\in \mathcal {A}$
is positive, and
$a\in \mathcal {A}$
is positive, and
![]() $p, q$
are distinct positive integers. Then the following conditions are equivalent:
$p, q$
are distinct positive integers. Then the following conditions are equivalent:
-
(i)
 $\varPhi $
restricted to the unital subalgebra generated by
$\varPhi $
restricted to the unital subalgebra generated by
 $\{a\}$
is multiplicative.
$\{a\}$
is multiplicative. -
(ii) There exists a positive element
 $b\in \mathcal {B}$
such that
$b\in \mathcal {B}$
such that
 $b^k=\varPhi (a^k)$
, for
$b^k=\varPhi (a^k)$
, for
 $k=p,q$
.
$k=p,q$
.
Moreover, if (ii) holds, then
![]() $b=\varPhi (a)$
.
$b=\varPhi (a)$
.
Proof It suffices to show the implication (ii)
![]() $\Rightarrow $
(i). Its proof is the same as that of Theorem 1.8, except that we use Theorem 1.3 instead of Theorem 1.7. We leave the details to the reader.
$\Rightarrow $
(i). Its proof is the same as that of Theorem 1.8, except that we use Theorem 1.3 instead of Theorem 1.7. We leave the details to the reader.
Remark 4.5 If the element
![]() $a$
is invertible, then in this case we can give another proof of the implication (ii)
$a$
is invertible, then in this case we can give another proof of the implication (ii)
![]() $\Rightarrow $
(i) of Theorem 4.4, which relies on a result of Petz. Without loss of generality, we can assume that
$\Rightarrow $
(i) of Theorem 4.4, which relies on a result of Petz. Without loss of generality, we can assume that
![]() $0 < p < q$
. Since
$0 < p < q$
. Since
![]() $a$
is positive and invertible and
$a$
is positive and invertible and
![]() $\varPhi $
is a unital positive linear map, we deduce that
$\varPhi $
is a unital positive linear map, we deduce that
![]() $a^q$
and thus
$a^q$
and thus
![]() $\varPhi (a^q)$
are positive and invertible. Let
$\varPhi (a^q)$
are positive and invertible. Let
![]() $f\colon (0,\infty ) \to \mathbb {R}$
be the function given by
$f\colon (0,\infty ) \to \mathbb {R}$
be the function given by
![]() $f(x)=-x^{\frac {p}{q}}$
for
$f(x)=-x^{\frac {p}{q}}$
for
![]() $x\in (0,\infty )$
. It follows from [Reference Bhatia9, Theorems V.1.9 and V.2.5] that
$x\in (0,\infty )$
. It follows from [Reference Bhatia9, Theorems V.1.9 and V.2.5] that
![]() $f$
is an operator convex function. Using (ii) and the Stone–von Neumann functional calculus, we get
$f$
is an operator convex function. Using (ii) and the Stone–von Neumann functional calculus, we get
and
Consequently,
Combined with [Reference Petz42, Theorem] and the fact that
![]() $\varPhi $
is continuous (see [Reference Paulsen41, Corollary 2.9]), this implies that
$\varPhi $
is continuous (see [Reference Paulsen41, Corollary 2.9]), this implies that
![]() $\varPhi $
restricted to the unital
$\varPhi $
restricted to the unital
![]() $C^*$
-algebra generated by
$C^*$
-algebra generated by
![]() $\{a^{q}\}$
is multiplicative. Applying the Stone–von Neumann functional calculus and the Weierstrass approximation theorem, one can show that the unital
$\{a^{q}\}$
is multiplicative. Applying the Stone–von Neumann functional calculus and the Weierstrass approximation theorem, one can show that the unital
![]() $C^*$
-algebras generated by
$C^*$
-algebras generated by
![]() $\{a\}$
and
$\{a\}$
and
![]() $\{a^{q}\}$
coincide (in fact, this is a very special case of the Müntz–Szász theorem; see [Reference Rudin47, Theorem 15.26]). Hence, (i) holds.
$\{a^{q}\}$
coincide (in fact, this is a very special case of the Müntz–Szász theorem; see [Reference Rudin47, Theorem 15.26]). Hence, (i) holds.
5 Proof of Theorem 1.9
We begin with a simple observation related to Problems 1.4 and 1.5. Namely, if
![]() $T$
and
$T$
and
![]() $F$
satisfy (1.3), then by (2.1) and the measure transport theorem for every
$F$
satisfy (1.3), then by (2.1) and the measure transport theorem for every
![]() $\tau \in \mathbb {R}\backslash \{0\}$
,
$\tau \in \mathbb {R}\backslash \{0\}$
,
![]() $\tau T$
and
$\tau T$
and
![]() $F_{\tau }$
satisfy (1.3), where
$F_{\tau }$
satisfy (1.3), where
![]() $F_{\tau }\colon \mathfrak {B}(\mathbb {R})\to \boldsymbol {B}(\mathcal {H})$
is the semispectral measure with compact support given by
$F_{\tau }\colon \mathfrak {B}(\mathbb {R})\to \boldsymbol {B}(\mathcal {H})$
is the semispectral measure with compact support given by
Moreover,
![]() $F$
is spectral if and only if
$F$
is spectral if and only if
![]() $F_{\tau }$
is spectral. A similar observation applies to Problem 1.5. In other words, rescaling preserves the affirmative or negative solutions to Problems 1.4 and 1.5.
$F_{\tau }$
is spectral. A similar observation applies to Problem 1.5. In other words, rescaling preserves the affirmative or negative solutions to Problems 1.4 and 1.5.
Next, we prove a lemma that is central to the proof of Theorem 5.2.
Lemma 5.1 Suppose that
![]() $(p,q)\in \mathbb {N}^2\backslash \varOmega $
and
$(p,q)\in \mathbb {N}^2\backslash \varOmega $
and
![]() $p\leqslant q$
, where
$p\leqslant q$
, where
![]() $\varOmega $
is as in (1.4). Then, for every
$\varOmega $
is as in (1.4). Then, for every
![]() $\tau \in \mathbb {R} \backslash \{0\}$
, there exist
$\tau \in \mathbb {R} \backslash \{0\}$
, there exist
![]() $\alpha ,\beta \in (0,1)$
and distinct
$\alpha ,\beta \in (0,1)$
and distinct
![]() $\lambda _1, \lambda _2\in \mathbb {R}$
such that
$\lambda _1, \lambda _2\in \mathbb {R}$
such that
 $$ \begin{align} \left\{ \begin{array}{ll} \alpha+\beta=1, \\[.5ex] \alpha\lambda_1^p+\beta\lambda_2^p=\tau^p, \\[.5ex] \alpha\lambda_1^q+\beta\lambda_2^q=\tau^q. \end{array} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{ll} \alpha+\beta=1, \\[.5ex] \alpha\lambda_1^p+\beta\lambda_2^p=\tau^p, \\[.5ex] \alpha\lambda_1^q+\beta\lambda_2^q=\tau^q. \end{array} \right. \end{align} $$
Proof We may assume, without loss of generality, that
![]() $\tau =1$
. Using the substitution
$\tau =1$
. Using the substitution
with
![]() $a,b \in (0,\infty )$
, we obtain an equivalent system of equations:
$a,b \in (0,\infty )$
, we obtain an equivalent system of equations:
 $$ \begin{align*} \left\{ \begin{array}{ll} \frac{a}{a+b} \lambda_1^p + \frac{b}{a+b} \lambda_2^p = 1, \\[.5ex] \frac{a}{a+b} \lambda_1^q + \frac{b}{a+b} \lambda_2^q=1. \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{ll} \frac{a}{a+b} \lambda_1^p + \frac{b}{a+b} \lambda_2^p = 1, \\[.5ex] \frac{a}{a+b} \lambda_1^q + \frac{b}{a+b} \lambda_2^q=1. \end{array} \right. \end{align*} $$
Multiplying both sides of the above equalities by
![]() $a+b$
and rearranging gives
$a+b$
and rearranging gives
 $$ \begin{align} \left\{ \begin{array}{ll} {a}(\lambda_1^p-1)+{b}(\lambda_2^p-1)=0, \\[.5ex] {a}(\lambda_1^q-1)+{b}(\lambda_2^q-1)=0. \end{array} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{ll} {a}(\lambda_1^p-1)+{b}(\lambda_2^p-1)=0, \\[.5ex] {a}(\lambda_1^q-1)+{b}(\lambda_2^q-1)=0. \end{array} \right. \end{align} $$
The determinant of the above system of equations (with unknowns
![]() $a,b$
) is
$a,b$
) is
 $$ \begin{align*} D(\lambda_1,\lambda_2) =\det \left[ \begin{matrix} \lambda_1^p-1 & \lambda_2^p-1 \\[.5ex] \lambda_1^q-1 & \lambda_2^q-1 \end{matrix} \right] = (\lambda_1^p-1) (\lambda_2^q-1)-(\lambda_2^p-1)( \lambda_1^q-1). \end{align*} $$
$$ \begin{align*} D(\lambda_1,\lambda_2) =\det \left[ \begin{matrix} \lambda_1^p-1 & \lambda_2^p-1 \\[.5ex] \lambda_1^q-1 & \lambda_2^q-1 \end{matrix} \right] = (\lambda_1^p-1) (\lambda_2^q-1)-(\lambda_2^p-1)( \lambda_1^q-1). \end{align*} $$
Observe that if
![]() $D(\lambda _1,\lambda _2) \neq 0$
, then the system of equations (5.2) has only one solution
$D(\lambda _1,\lambda _2) \neq 0$
, then the system of equations (5.2) has only one solution
![]() $a=b=0$
. Thus, the only chance to find nonzero solutions
$a=b=0$
. Thus, the only chance to find nonzero solutions
![]() $a, b$
of the system (5.2) is when
$a, b$
of the system (5.2) is when
![]() $D(\lambda _1,\lambda _2)=0$
. Note that
$D(\lambda _1,\lambda _2)=0$
. Note that
 $$ \begin{align} \textit{if} \ \lambda_1,\lambda_2\in \mathbb{R}\backslash\{-1,1\}, \ \textit{then} \ D(\lambda_1,\lambda_2)=0 \ \textit{if and only if} \ \frac{\lambda_1^p-1}{\lambda_1^q-1} = \frac{\lambda_2^p-1}{\lambda_2^q-1}. \end{align} $$
$$ \begin{align} \textit{if} \ \lambda_1,\lambda_2\in \mathbb{R}\backslash\{-1,1\}, \ \textit{then} \ D(\lambda_1,\lambda_2)=0 \ \textit{if and only if} \ \frac{\lambda_1^p-1}{\lambda_1^q-1} = \frac{\lambda_2^p-1}{\lambda_2^q-1}. \end{align} $$
We will consider four cases.
Case 1.
![]() $p=q$
.
$p=q$
.
It is easily seen that for any
![]() $\alpha , \beta \in (0,1)$
such that
$\alpha , \beta \in (0,1)$
such that
![]() $\alpha + \beta =1$
, there are plenty of two-element subsets
$\alpha + \beta =1$
, there are plenty of two-element subsets
![]() $\{\lambda _1,\lambda _2\}$
of
$\{\lambda _1,\lambda _2\}$
of
![]() $(0,\infty )$
solving (5.1).
$(0,\infty )$
solving (5.1).
Case 2. Both
![]() $p$
and
$p$
and
![]() $q$
are even.
$q$
are even.
Set
![]() $\lambda _1=-1$
,
$\lambda _1=-1$
,
![]() $\lambda _2=1$
, and
$\lambda _2=1$
, and
![]() $\beta =1-\alpha $
, where
$\beta =1-\alpha $
, where
![]() $\alpha \in (0,1)$
. Then it is easily seen that (5.1) is satisfied.
$\alpha \in (0,1)$
. Then it is easily seen that (5.1) is satisfied.
Case 3.
![]() $p<q$
,
$p<q$
,
![]() $p$
is even, and
$p$
is even, and
![]() $q$
is odd.
$q$
is odd.
Consider the function
![]() $\phi \colon [0,1]\to [0,1]$
defined by
$\phi \colon [0,1]\to [0,1]$
defined by
Then
![]() $\phi $
is continuous,
$\phi $
is continuous,
![]() $\phi (0)=1$
,
$\phi (0)=1$
,
![]() $\phi (1)=0$
, and
$\phi (1)=0$
, and
![]() $\phi ((0,1)) \subseteq (0,1)$
. By the Darboux property of continuous functions,
$\phi ((0,1)) \subseteq (0,1)$
. By the Darboux property of continuous functions,
![]() $\phi ((0,1))=(0,1)$
. Take
$\phi ((0,1))=(0,1)$
. Take
![]() $\lambda _1>1$
. Then
$\lambda _1>1$
. Then
 $$ \begin{align*} \frac{1-\lambda_1^p}{1-\lambda_1^q}\in (0,1). \end{align*} $$
$$ \begin{align*} \frac{1-\lambda_1^p}{1-\lambda_1^q}\in (0,1). \end{align*} $$
Therefore, there exists
![]() $x\in (0,1)$
such that
$x\in (0,1)$
such that
 $$ \begin{align} \frac{1-\lambda_1^p}{1-\lambda_1^q}=\phi(x). \end{align} $$
$$ \begin{align} \frac{1-\lambda_1^p}{1-\lambda_1^q}=\phi(x). \end{align} $$
Set
![]() $\lambda _2=-x$
. Then
$\lambda _2=-x$
. Then
![]() $\lambda _2<0$
,
$\lambda _2<0$
,
![]() $|\lambda _2|=x<1$
and
$|\lambda _2|=x<1$
and
 $$ \begin{align*} \frac{1-\lambda_1^p}{1-\lambda_1^q} \overset{(5.4)}{=} \frac{1-|\lambda_2|^p} {1+|\lambda_2|^q} = \frac{1-\lambda_2^p}{1-\lambda_2^q}, \end{align*} $$
$$ \begin{align*} \frac{1-\lambda_1^p}{1-\lambda_1^q} \overset{(5.4)}{=} \frac{1-|\lambda_2|^p} {1+|\lambda_2|^q} = \frac{1-\lambda_2^p}{1-\lambda_2^q}, \end{align*} $$
which by (5.3) means that
![]() $D(\lambda _1,\lambda _2)=0$
, so the system of equations (5.2) is linearly dependent. Take any
$D(\lambda _1,\lambda _2)=0$
, so the system of equations (5.2) is linearly dependent. Take any
![]() $a\in (0,\infty )$
and set
$a\in (0,\infty )$
and set
 $$ \begin{align*} b=a\frac{\lambda_1^p-1}{1-\lambda_2^p}>0. \end{align*} $$
$$ \begin{align*} b=a\frac{\lambda_1^p-1}{1-\lambda_2^p}>0. \end{align*} $$
Then the pair
![]() $(a,b)$
is a solution of the system of equations (5.2).
$(a,b)$
is a solution of the system of equations (5.2).
Case 4.
![]() $p<q$
and both
$p<q$
and both
![]() $p$
and
$p$
and
![]() $q$
are odd.
$q$
are odd.
Consider the function
![]() $\psi \colon [1,\infty )\to (0,1]$
defined by
$\psi \colon [1,\infty )\to (0,1]$
defined by
Then
![]() $\psi $
is continuous,
$\psi $
is continuous,
![]() $\psi (1)=1$
,
$\psi (1)=1$
,
![]() $\lim _{x\to \infty }\psi (x)=0$
, and
$\lim _{x\to \infty }\psi (x)=0$
, and
![]() $\psi ((1,\infty ))\subseteq (0,1)$
. As a consequence of the Darboux property of continuous functions,
$\psi ((1,\infty ))\subseteq (0,1)$
. As a consequence of the Darboux property of continuous functions,
![]() $\psi ((1,\infty ))=(0,1)$
. Take
$\psi ((1,\infty ))=(0,1)$
. Take
![]() $\lambda _1>1$
. Observe that
$\lambda _1>1$
. Observe that
 $$ \begin{align*} \frac{1-\lambda_1^p}{1-\lambda_1^q}\in (0,1). \end{align*} $$
$$ \begin{align*} \frac{1-\lambda_1^p}{1-\lambda_1^q}\in (0,1). \end{align*} $$
Hence, there exists
![]() $x\in (1,\infty )$
such that
$x\in (1,\infty )$
such that
 $$ \begin{align} \frac{1-\lambda_1^p}{1-\lambda_1^q}=\psi(x). \end{align} $$
$$ \begin{align} \frac{1-\lambda_1^p}{1-\lambda_1^q}=\psi(x). \end{align} $$
Set
![]() $\lambda _2=-x$
. Then
$\lambda _2=-x$
. Then
![]() $\lambda _2<0$
,
$\lambda _2<0$
,
![]() $|\lambda _2|=x>1$
, and
$|\lambda _2|=x>1$
, and
 $$ \begin{align*} \frac{1-\lambda_1^p} {1-\lambda_1^q} \overset{(5.5)}{=} \psi(|\lambda_2|) = \frac{1+|\lambda_2|^p} {1+|\lambda_2|^q} = \frac{1-\lambda_2^p}{1-\lambda_2^q}. \end{align*} $$
$$ \begin{align*} \frac{1-\lambda_1^p} {1-\lambda_1^q} \overset{(5.5)}{=} \psi(|\lambda_2|) = \frac{1+|\lambda_2|^p} {1+|\lambda_2|^q} = \frac{1-\lambda_2^p}{1-\lambda_2^q}. \end{align*} $$
As in Case 3, taking any
![]() $a\in (0,\infty )$
and setting
$a\in (0,\infty )$
and setting
 $$ \begin{align*} b=a\frac{\lambda_1^p-1}{1-\lambda_2^p} = a \frac{\lambda_1^p-1} {1+|\lambda_2|^p}>0, \end{align*} $$
$$ \begin{align*} b=a\frac{\lambda_1^p-1}{1-\lambda_2^p} = a \frac{\lambda_1^p-1} {1+|\lambda_2|^p}>0, \end{align*} $$
we see that the pair
![]() $(a,b)$
is a solution of the system of equations (5.2). This completes the proof.
$(a,b)$
is a solution of the system of equations (5.2). This completes the proof.
We are now ready to prove the main result of this section, which provides the counterexamples mentioned earlier in the Introduction. In fact, this is a stronger version of Theorem 1.9.
Theorem 5.2 Suppose that
![]() $(p,q)\in \mathbb {N}^2\backslash \varOmega $
and
$(p,q)\in \mathbb {N}^2\backslash \varOmega $
and
![]() $p\leqslant q$
, where
$p\leqslant q$
, where
![]() $\varOmega $
is as in (1.4). Let
$\varOmega $
is as in (1.4). Let
![]() $\tau \in \mathbb {R}\backslash \{0\}$
. Set
$\tau \in \mathbb {R}\backslash \{0\}$
. Set
![]() $\mathcal {H}=\mathbb {C}$
and
$\mathcal {H}=\mathbb {C}$
and
![]() $T=\tau I$
. Then there exist
$T=\tau I$
. Then there exist
![]() $\alpha ,\beta \in (0,1)$
and
$\alpha ,\beta \in (0,1)$
and
![]() $\lambda _1, \lambda _2\in \mathbb {R}$
such that
$\lambda _1, \lambda _2\in \mathbb {R}$
such that
![]() $\alpha +\beta =1$
,
$\alpha +\beta =1$
,
![]() $\lambda _1 \neq \lambda _2$
and
$\lambda _1 \neq \lambda _2$
and
-
(i) the semispectral measure
 $F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
defined by (5.6)is not spectral and
$F\colon \mathfrak {B}(\mathbb {R}) \to \boldsymbol {B}(\mathcal {H})$
defined by (5.6)is not spectral and $$ \begin{align} F(\varDelta) = \alpha\delta_{\lambda_1} (\varDelta) I + \beta \delta_{\lambda_2} (\varDelta)I, \quad \varDelta \in \mathfrak{B}(\mathbb{R}), \end{align} $$
(5.7)
$$ \begin{align} F(\varDelta) = \alpha\delta_{\lambda_1} (\varDelta) I + \beta \delta_{\lambda_2} (\varDelta)I, \quad \varDelta \in \mathfrak{B}(\mathbb{R}), \end{align} $$
(5.7) $$ \begin{align} T^k=\int_{\mathbb{R}} x^k F(\mathrm{d\hspace{.1ex}} x), \quad k=p,q, \end{align} $$
$$ \begin{align} T^k=\int_{\mathbb{R}} x^k F(\mathrm{d\hspace{.1ex}} x), \quad k=p,q, \end{align} $$
-
(ii) the self-adjoint operator
 $S\in \boldsymbol {B}(\mathcal {H}\oplus \mathcal {H})$
defined by does not commute with
$S\in \boldsymbol {B}(\mathcal {H}\oplus \mathcal {H})$
defined by does not commute with $$ \begin{align*} S = \left[ \begin{matrix} \alpha \lambda_1 + \beta \lambda_2 & \sqrt{\alpha\beta} (\lambda_1 - \lambda_2) \\[1ex] \sqrt{\alpha\beta}(\lambda_1-\lambda_2) & \beta\lambda_1+\alpha\lambda_2 \end{matrix} \right] \end{align*} $$
$$ \begin{align*} S = \left[ \begin{matrix} \alpha \lambda_1 + \beta \lambda_2 & \sqrt{\alpha\beta} (\lambda_1 - \lambda_2) \\[1ex] \sqrt{\alpha\beta}(\lambda_1-\lambda_2) & \beta\lambda_1+\alpha\lambda_2 \end{matrix} \right] \end{align*} $$
 $P:=\big [ \begin {smallmatrix} 1 & 0 \\0 & 0 \end {smallmatrix}\big ]$
and (5.8)
$P:=\big [ \begin {smallmatrix} 1 & 0 \\0 & 0 \end {smallmatrix}\big ]$
and (5.8) $$ \begin{align} T^k = P S^k|_{\mathcal{H}}, \quad k=p,q, \end{align} $$
$$ \begin{align} T^k = P S^k|_{\mathcal{H}}, \quad k=p,q, \end{align} $$
-
(iii) the unital positive linear map
 $\varPhi \colon C(K) \to \boldsymbol {B}(\mathcal {H})$
defined by (5.9)is not multiplicative,
$\varPhi \colon C(K) \to \boldsymbol {B}(\mathcal {H})$
defined by (5.9)is not multiplicative, $$ \begin{align} \varPhi(f) = \int_{K} f \mathrm{d\hspace{.1ex}} F, \quad f \in C(K), \end{align} $$
$$ \begin{align} \varPhi(f) = \int_{K} f \mathrm{d\hspace{.1ex}} F, \quad f \in C(K), \end{align} $$
 $C(K)$
is the unital algebra generated by
$C(K)$
is the unital algebra generated by
 $\{a\}$
, and (5.10)where
$\{a\}$
, and (5.10)where $$ \begin{align} b^k=\varPhi(a^k), \quad k=p,q, \end{align} $$
$$ \begin{align} b^k=\varPhi(a^k), \quad k=p,q, \end{align} $$
 $F$
is as in (5.6),
$F$
is as in (5.6),
 $K=\{\lambda _1,\lambda _2\}$
,
$K=\{\lambda _1,\lambda _2\}$
,
 $a(x)=x$
for
$a(x)=x$
for
 $x\in K$
, and
$x\in K$
, and
 $b= T$
.
$b= T$
.
Proof Let
![]() $\alpha ,\beta ,\lambda _1,\lambda _2$
be as in Lemma 5.1.
$\alpha ,\beta ,\lambda _1,\lambda _2$
be as in Lemma 5.1.
(i) By (5.1) and (5.6),
![]() $F$
is a semispectral measure satisfying (5.7). However,
$F$
is a semispectral measure satisfying (5.7). However,
![]() $F$
is not a spectral measure because
$F$
is not a spectral measure because
![]() $F(\{\lambda _1\})=\alpha I$
and
$F(\{\lambda _1\})=\alpha I$
and
![]() $\alpha \in (0,1)$
.
$\alpha \in (0,1)$
.
(ii) Clearly, the operator
![]() $S$
is self-adjoint. It follows from the first equality in (5.1) that the matrix
$S$
is self-adjoint. It follows from the first equality in (5.1) that the matrix
 $$ \begin{align*} \left[ \begin{matrix} \sqrt{\alpha} & \sqrt{\beta} \\[1ex] -\sqrt{\beta} & \sqrt{\alpha} \end{matrix} \right] \end{align*} $$
$$ \begin{align*} \left[ \begin{matrix} \sqrt{\alpha} & \sqrt{\beta} \\[1ex] -\sqrt{\beta} & \sqrt{\alpha} \end{matrix} \right] \end{align*} $$
is unitary and consequently
 $$ \begin{align} \left[ \begin{matrix} \sqrt{\alpha} & \sqrt{\beta} \\[1ex] -\sqrt{\beta} & \sqrt{\alpha} \end{matrix} \right]^{-1} = \left[ \begin{matrix} \sqrt{\alpha} & -\sqrt{\beta} \\[1ex] \sqrt{\beta} & \sqrt{\alpha} \end{matrix} \right]. \end{align} $$
$$ \begin{align} \left[ \begin{matrix} \sqrt{\alpha} & \sqrt{\beta} \\[1ex] -\sqrt{\beta} & \sqrt{\alpha} \end{matrix} \right]^{-1} = \left[ \begin{matrix} \sqrt{\alpha} & -\sqrt{\beta} \\[1ex] \sqrt{\beta} & \sqrt{\alpha} \end{matrix} \right]. \end{align} $$
Now, it is easily seen that the Jordan decomposition of
![]() $S$
takes the form
$S$
takes the form
 $$ \begin{align*} S = \left[ \begin{matrix} \sqrt{\alpha} & -\sqrt{\beta} \\[1ex] \sqrt{\beta} & \sqrt{\alpha} \end{matrix} \right] \left[ \begin{matrix} \lambda_1 & 0 \\[1ex] 0 & \lambda_2 \end{matrix} \right] \left[ \begin{matrix} \sqrt{\alpha} & \sqrt{\beta} \\[1ex] -\sqrt{\beta} & \sqrt{\alpha} \end{matrix} \right]. \end{align*} $$
$$ \begin{align*} S = \left[ \begin{matrix} \sqrt{\alpha} & -\sqrt{\beta} \\[1ex] \sqrt{\beta} & \sqrt{\alpha} \end{matrix} \right] \left[ \begin{matrix} \lambda_1 & 0 \\[1ex] 0 & \lambda_2 \end{matrix} \right] \left[ \begin{matrix} \sqrt{\alpha} & \sqrt{\beta} \\[1ex] -\sqrt{\beta} & \sqrt{\alpha} \end{matrix} \right]. \end{align*} $$
Combined with (5.11), this implies that
 $$ \begin{align} S^n = \left[ \begin{matrix} \alpha\lambda_1^n+\beta\lambda_2^n & \sqrt{\alpha\beta} (\lambda_1^n-\lambda_2^n) \\[1ex] \sqrt{\alpha\beta}(\lambda_1^n-\lambda_2^n) & \beta\lambda_1^n+\alpha\lambda_2^n \end{matrix} \right], \quad n \in \mathbb{Z}_+. \end{align} $$
$$ \begin{align} S^n = \left[ \begin{matrix} \alpha\lambda_1^n+\beta\lambda_2^n & \sqrt{\alpha\beta} (\lambda_1^n-\lambda_2^n) \\[1ex] \sqrt{\alpha\beta}(\lambda_1^n-\lambda_2^n) & \beta\lambda_1^n+\alpha\lambda_2^n \end{matrix} \right], \quad n \in \mathbb{Z}_+. \end{align} $$
By (5.1) and (5.12), the condition (5.8) is satisfied. Since
![]() $\lambda _1\neq \lambda _2$
, the operator
$\lambda _1\neq \lambda _2$
, the operator
![]() $S$
does not commute with
$S$
does not commute with
![]() $P$
.
$P$
.
(iii) It is immediate from (5.9) and (i) that
![]() $\varPhi $
is the unital positive linear map which satisfies (5.10). Clearly,
$\varPhi $
is the unital positive linear map which satisfies (5.10). Clearly,
![]() $C(K)$
is the unital algebra generated by
$C(K)$
is the unital algebra generated by
![]() $\{a\}$
. To show that
$\{a\}$
. To show that
![]() $\varPhi $
is not multiplicative, consider two polynomials
$\varPhi $
is not multiplicative, consider two polynomials
![]() $u(x) = x-\lambda _1$
and
$u(x) = x-\lambda _1$
and
![]() $v(x)=x-\lambda _2$
and note that
$v(x)=x-\lambda _2$
and note that
![]() $\varPhi (u(a)v(a))=0$
while
$\varPhi (u(a)v(a))=0$
while
![]() $\varPhi (u(a)) \varPhi (v(a)) = - \alpha \beta (\lambda _1 - \lambda _2)^2 \neq 0$
. This completes the proof.
$\varPhi (u(a)) \varPhi (v(a)) = - \alpha \beta (\lambda _1 - \lambda _2)^2 \neq 0$
. This completes the proof.
Remark 5.3 A careful inspection of the proofs of Lemma 5.1 and Theorem 5.2 shows that there is great freedom in the choice of the parameters
![]() $\lambda _1$
and
$\lambda _1$
and
![]() $\lambda _2$
; however, if
$\lambda _2$
; however, if
![]() $p < q$
and
$p < q$
and
![]() $\tau> 0$
, then in view of [Reference Pietrzycki and Stochel43, Theorem 4.2], at least one of these parameters must be negative. Note also that if
$\tau> 0$
, then in view of [Reference Pietrzycki and Stochel43, Theorem 4.2], at least one of these parameters must be negative. Note also that if
![]() $p<q$
,
$p<q$
,
![]() $p$
is odd, and
$p$
is odd, and
![]() $q$
is even, then according to Theorems 1.7 and 1.8, there are no
$q$
is even, then according to Theorems 1.7 and 1.8, there are no
![]() $\alpha ,\beta , \lambda _1, \lambda _2$
satisfying the conclusion of Theorem 5.2. In this particular case, we can justify it in an elementary way. Namely, by the Hölder inequality, we infer from (5.1) that
$\alpha ,\beta , \lambda _1, \lambda _2$
satisfying the conclusion of Theorem 5.2. In this particular case, we can justify it in an elementary way. Namely, by the Hölder inequality, we infer from (5.1) that
 $$ \begin{align} \notag |\tau|^p= |\alpha\lambda_1^p+\beta\lambda_2^p| & \leqslant \alpha|\lambda_1|^p+\beta|\lambda_2|^p \\ \notag & \leqslant \sqrt[r]{\alpha+\beta}\, \sqrt[q/p]{ \alpha|\lambda_1|^q+\beta|\lambda_2|^q} \\ & = \sqrt[r]{\alpha+\beta}\, \sqrt[q/p]{ \alpha\lambda_1^q+\beta\lambda_2^q}= |\tau|^p, \end{align} $$
$$ \begin{align} \notag |\tau|^p= |\alpha\lambda_1^p+\beta\lambda_2^p| & \leqslant \alpha|\lambda_1|^p+\beta|\lambda_2|^p \\ \notag & \leqslant \sqrt[r]{\alpha+\beta}\, \sqrt[q/p]{ \alpha|\lambda_1|^q+\beta|\lambda_2|^q} \\ & = \sqrt[r]{\alpha+\beta}\, \sqrt[q/p]{ \alpha\lambda_1^q+\beta\lambda_2^q}= |\tau|^p, \end{align} $$
where
![]() $r\in (1,\infty )$
is such that
$r\in (1,\infty )$
is such that
![]() $\frac {1}{r}+\frac {p}{q}=1$
. This means that equality in the Hölder inequality holds. As a consequence, we deduce that
$\frac {1}{r}+\frac {p}{q}=1$
. This means that equality in the Hölder inequality holds. As a consequence, we deduce that
![]() $|\lambda _1|=|\lambda _2|$
. Combined with the first inequality in (5.13) and the assumption that
$|\lambda _1|=|\lambda _2|$
. Combined with the first inequality in (5.13) and the assumption that
![]() $p$
is odd, this implies that
$p$
is odd, this implies that
![]() $\lambda _1=\lambda _2$
, which is a contradiction.
$\lambda _1=\lambda _2$
, which is a contradiction.
6 More examples
In this section, we illustrate Theorem 1.9 (cf. Theorem 5.2) with two interesting examples for the case
![]() $(p,q)=(2,3)$
. Now, we use the dilation approach as stated in Lemma 3.2 (cf. Problems 1.4 and 1.5).
$(p,q)=(2,3)$
. Now, we use the dilation approach as stated in Lemma 3.2 (cf. Problems 1.4 and 1.5).
Example 6.1 Let
![]() $\{f_n\}_{n=0}^{\infty }$
be the Fibonacci sequence, that is,
$\{f_n\}_{n=0}^{\infty }$
be the Fibonacci sequence, that is,
![]() $f_0=0$
,
$f_0=0$
,
![]() $f_1=1$
, and
$f_1=1$
, and
![]() $f_{n+1}=f_n+f_{n-1}$
for
$f_{n+1}=f_n+f_{n-1}$
for
![]() $n\in \mathbb {N}$
. It is well known and easy to prove that
$n\in \mathbb {N}$
. It is well known and easy to prove that
 $$ \begin{align} \left[ \begin{matrix} 0 & 1 \\ 1 & 1 \end{matrix} \right]^n=\left[ \begin{matrix} f_{n-1} & f_{n}\\ f_{n} & f_{n+1} \end{matrix} \right], \quad n \in \mathbb{N}. \end{align} $$
$$ \begin{align} \left[ \begin{matrix} 0 & 1 \\ 1 & 1 \end{matrix} \right]^n=\left[ \begin{matrix} f_{n-1} & f_{n}\\ f_{n} & f_{n+1} \end{matrix} \right], \quad n \in \mathbb{N}. \end{align} $$
Set
![]() $\mathcal {H}=\mathbb {C}$
,
$\mathcal {H}=\mathbb {C}$
,
![]() $T=I$
, and
$T=I$
, and
 $$ \begin{align*} S= \left[ \begin{matrix} 0 & 1 \\ 1 & 1 \end{matrix} \right]. \end{align*} $$
$$ \begin{align*} S= \left[ \begin{matrix} 0 & 1 \\ 1 & 1 \end{matrix} \right]. \end{align*} $$
Then
![]() $S$
is a self-adjoint operator and the spectral measure
$S$
is a self-adjoint operator and the spectral measure
![]() $E$
of
$E$
of
![]() $S$
is given by
$S$
is given by
 $$ \begin{align*} E(\varDelta) = \frac{1}{1+\phi^2} \delta_{1-\phi} (\varDelta) \left[ \begin{matrix} \phi^2 & - \phi \\ - \phi & 1 \end{matrix} \right] + \frac{1}{1+\phi^2} \delta_{\phi} (\varDelta) \left[ \begin{matrix} 1 & \phi \\ \phi & \phi^2 \end{matrix} \right], \quad \varDelta \in \mathfrak{B}(\mathbb{R}), \end{align*} $$
$$ \begin{align*} E(\varDelta) = \frac{1}{1+\phi^2} \delta_{1-\phi} (\varDelta) \left[ \begin{matrix} \phi^2 & - \phi \\ - \phi & 1 \end{matrix} \right] + \frac{1}{1+\phi^2} \delta_{\phi} (\varDelta) \left[ \begin{matrix} 1 & \phi \\ \phi & \phi^2 \end{matrix} \right], \quad \varDelta \in \mathfrak{B}(\mathbb{R}), \end{align*} $$
where
![]() $\phi =\frac {1+\sqrt {5}}{2}$
is the golden ratio. It follows from (6.1) that
$\phi =\frac {1+\sqrt {5}}{2}$
is the golden ratio. It follows from (6.1) that
where
![]() $P= \left [ \begin {smallmatrix} 1 & 0 \\ 0 & 0 \end {smallmatrix} \right ]$
is the orthogonal projection of
$P= \left [ \begin {smallmatrix} 1 & 0 \\ 0 & 0 \end {smallmatrix} \right ]$
is the orthogonal projection of
![]() $\mathcal {H} \oplus \mathcal {H}$
onto
$\mathcal {H} \oplus \mathcal {H}$
onto
![]() $\mathcal {H}$
. The semispectral measure
$\mathcal {H}$
. The semispectral measure
![]() $F:=PE|_{\mathcal {H}}$
(see (3.2) for the definition of
$F:=PE|_{\mathcal {H}}$
(see (3.2) for the definition of
![]() $PE|_{\mathcal {H}}$
) takes the form
$PE|_{\mathcal {H}}$
) takes the form
 $$ \begin{align} F(\varDelta) = \frac{\phi^2}{1+\phi^2} \delta_{1-\phi} (\varDelta)I + \frac{1}{1+\phi^2} \delta_{\phi} (\varDelta) I, \quad \varDelta \in \mathfrak{B}(\mathbb{R}). \end{align} $$
$$ \begin{align} F(\varDelta) = \frac{\phi^2}{1+\phi^2} \delta_{1-\phi} (\varDelta)I + \frac{1}{1+\phi^2} \delta_{\phi} (\varDelta) I, \quad \varDelta \in \mathfrak{B}(\mathbb{R}). \end{align} $$
By Lemma 3.2(ii), we have
Clearly, by (6.2),
![]() $F$
is not a spectral measure (also because
$F$
is not a spectral measure (also because
![]() $P$
does not commute with
$P$
does not commute with
![]() $S$
; see Lemma 3.2).
$S$
; see Lemma 3.2).
The next example is a modification of the previous one.
Example 6.2 Let
![]() $T\in \boldsymbol {B}(\mathcal {H})$
be a nonzero self-adjoint operator, and let
$T\in \boldsymbol {B}(\mathcal {H})$
be a nonzero self-adjoint operator, and let
![]() $S\in \boldsymbol {B}(\mathcal {H}\oplus \mathcal {H})$
be the self-adjoint operator given by the
$S\in \boldsymbol {B}(\mathcal {H}\oplus \mathcal {H})$
be the self-adjoint operator given by the
![]() $2 \times 2$
block matrix
$2 \times 2$
block matrix
 $$ \begin{align} S= \left[ \begin{matrix} 0 & T \\ T & T \end{matrix} \right]. \end{align} $$
$$ \begin{align} S= \left[ \begin{matrix} 0 & T \\ T & T \end{matrix} \right]. \end{align} $$
One can verify that
 $$ \begin{align*} S^2=\left[ \begin{matrix} T^2 & T^2 \\ T^2 & 2T^2 \end{matrix} \right] \quad \text{and} \quad S^3=\left[ \begin{matrix} T^3 & 2T^3 \\ 2T^3 & 3T^3 \end{matrix} \right]. \end{align*} $$
$$ \begin{align*} S^2=\left[ \begin{matrix} T^2 & T^2 \\ T^2 & 2T^2 \end{matrix} \right] \quad \text{and} \quad S^3=\left[ \begin{matrix} T^3 & 2T^3 \\ 2T^3 & 3T^3 \end{matrix} \right]. \end{align*} $$
Thus, the operators
![]() $T$
and
$T$
and
![]() $S$
satisfy the following two identities:
$S$
satisfy the following two identities:
where
![]() $P= \left [ \begin {smallmatrix} I_{\mathcal {H}} & 0 \\ 0 & 0 \end {smallmatrix} \right ]$
is the orthogonal projection of
$P= \left [ \begin {smallmatrix} I_{\mathcal {H}} & 0 \\ 0 & 0 \end {smallmatrix} \right ]$
is the orthogonal projection of
![]() $\mathcal {H}\oplus \mathcal {H}$
onto
$\mathcal {H}\oplus \mathcal {H}$
onto
![]() $\mathcal {H}$
. Let
$\mathcal {H}$
. Let
![]() $E$
be the spectral measure of
$E$
be the spectral measure of
![]() $S$
, and let
$S$
, and let
![]() $F:=PE|_{\mathcal {H}}$
be the corresponding semispectral measure. Applying Lemma 3.2(ii) and using (6.4), we get
$F:=PE|_{\mathcal {H}}$
be the corresponding semispectral measure. Applying Lemma 3.2(ii) and using (6.4), we get
Since
![]() $T\neq 0$
, the operator
$T\neq 0$
, the operator
![]() $P$
does not commute with
$P$
does not commute with
![]() $S$
, so by Lemma 3.2,
$S$
, so by Lemma 3.2,
![]() $F$
is not a spectral measure. In contrast to Example 6.1, here it is much easier to use Lemma 3.2 to see that the semispectral measure
$F$
is not a spectral measure. In contrast to Example 6.1, here it is much easier to use Lemma 3.2 to see that the semispectral measure
![]() $F$
is not spectral.
$F$
is not spectral.
Remark 6.3 Regarding Example 6.2, note that the operator
![]() $S$
given by (6.3) is unitarily equivalent to the tensor product
$S$
given by (6.3) is unitarily equivalent to the tensor product
 $$ \begin{align*} S=\left[ \begin{matrix} 0 & 1 \\ 1 & 1 \end{matrix} \right] \otimes T. \end{align*} $$
$$ \begin{align*} S=\left[ \begin{matrix} 0 & 1 \\ 1 & 1 \end{matrix} \right] \otimes T. \end{align*} $$
Combined with (6.1), this implies that
 $$ \begin{align*} S^n=\left[ \begin{matrix} 0 & 1 \\ 1 & 1 \end{matrix} \right]^n \otimes T^n = \left[ \begin{matrix} f_{n-1} T^n & f_{n} T^n \\ f_{n} T^n & f_{n+1} T^n \end{matrix} \right], \quad n \in \mathbb{N}. \end{align*} $$
$$ \begin{align*} S^n=\left[ \begin{matrix} 0 & 1 \\ 1 & 1 \end{matrix} \right]^n \otimes T^n = \left[ \begin{matrix} f_{n-1} T^n & f_{n} T^n \\ f_{n} T^n & f_{n+1} T^n \end{matrix} \right], \quad n \in \mathbb{N}. \end{align*} $$
This means that tensoring and orthogonal summation enrich the class of counterexamples by allowing semispectral measures to have operator values on Hilbert spaces of arbitrary dimension.
7 Semispectral measures with noncompact supports
In this section, we extend the two-moment characterizations of spectral measures given in Theorems 1.3 and 1.7 to the case of semispectral measures with noncompact supports. When considering a Borel semispectral measure
![]() $F$
on the real line with noncompact support, it may happen that the coordinate function
$F$
on the real line with noncompact support, it may happen that the coordinate function
![]() $\mathbb {R} \ni x \mapsto x \in \mathbb {R}$
is not in
$\mathbb {R} \ni x \mapsto x \in \mathbb {R}$
is not in
![]() $L^1(F)$
(cf. (2.1)), which means that the expression
$L^1(F)$
(cf. (2.1)), which means that the expression
![]() $\int _{\mathbb {R}} x^k F(\mathrm {d\hspace {.1ex}} x)$
, where
$\int _{\mathbb {R}} x^k F(\mathrm {d\hspace {.1ex}} x)$
, where
![]() $k\in \mathbb {N}$
, may not yield a bounded operator. On the other hand, if Problem 1.4 has an affirmative solution under the formally weaker assumption that the functions
$k\in \mathbb {N}$
, may not yield a bounded operator. On the other hand, if Problem 1.4 has an affirmative solution under the formally weaker assumption that the functions
![]() $\mathbb {R} \ni x \mapsto x^k \in \mathbb {R}$
,
$\mathbb {R} \ni x \mapsto x^k \in \mathbb {R}$
,
![]() $k \in \varXi $
, are in
$k \in \varXi $
, are in
![]() $L^1(F)$
, then
$L^1(F)$
, then
![]() $F$
being a posteriori a spectral measure must have a compact support. Indeed, by the measure transport theorem
$F$
being a posteriori a spectral measure must have a compact support. Indeed, by the measure transport theorem
![]() $T^k = \int _{\mathbb {R}} x (F\circ \varphi _k^{-1})(\mathrm {d\hspace {.1ex}} x)$
, where
$T^k = \int _{\mathbb {R}} x (F\circ \varphi _k^{-1})(\mathrm {d\hspace {.1ex}} x)$
, where
![]() $\varphi _k$
is as in (3.7) and
$\varphi _k$
is as in (3.7) and
![]() $k$
is any element of
$k$
is any element of
![]() $\varXi $
, and thus
$\varXi $
, and thus
![]() $F\circ \varphi _k^{-1}$
is the spectral measure of the (bounded) self-adjoint operator
$F\circ \varphi _k^{-1}$
is the spectral measure of the (bounded) self-adjoint operator
![]() $T^k$
. Hence,
$T^k$
. Hence,
![]() $F\circ \varphi _k^{-1}$
must have compact support (see [Reference Schmüdgen48, Theorem 5.9]). Consequently,
$F\circ \varphi _k^{-1}$
must have compact support (see [Reference Schmüdgen48, Theorem 5.9]). Consequently,
![]() $F$
itself must have compact support. A similar argument applied in the case where a semispectral measure
$F$
itself must have compact support. A similar argument applied in the case where a semispectral measure
![]() $F\colon \mathscr {A} \to \boldsymbol {B}(\mathcal {H})$
is considered on an abstract measurable space
$F\colon \mathscr {A} \to \boldsymbol {B}(\mathcal {H})$
is considered on an abstract measurable space
![]() $(X,\mathscr {A})$
, and the coordinate function is replaced by a measurable real-valued function
$(X,\mathscr {A})$
, and the coordinate function is replaced by a measurable real-valued function
![]() $\omega $
on
$\omega $
on
![]() $X$
, leads to the conclusion that
$X$
, leads to the conclusion that
![]() $\omega $
is
$\omega $
is
![]() $F$
-essentially bounded, that is,
$F$
-essentially bounded, that is,
![]() $F(\{x\in X\colon |\omega (x)|> r\})=0$
for some
$F(\{x\in X\colon |\omega (x)|> r\})=0$
for some
![]() $r\in \mathbb {R}_+$
(equivalently,
$r\in \mathbb {R}_+$
(equivalently,
![]() $\omega \in L^{\infty }(F)$
). However, to get the spectrality of
$\omega \in L^{\infty }(F)$
). However, to get the spectrality of
![]() $F$
, it is not enough to assume that
$F$
, it is not enough to assume that
![]() $\omega $
is
$\omega $
is
![]() $F$
-essentially bounded. It turns out that the “missing” property of
$F$
-essentially bounded. It turns out that the “missing” property of
![]() $\omega $
is
$\omega $
is
![]() $\sigma $
-surjectivity. We say that a measurable map
$\sigma $
-surjectivity. We say that a measurable map
![]() $f\colon X \to Y$
between measurable spaces
$f\colon X \to Y$
between measurable spaces
![]() $(X, \mathscr {A})$
and
$(X, \mathscr {A})$
and
![]() $(Y,\mathscr {B})$
(i.e., a map such that
$(Y,\mathscr {B})$
(i.e., a map such that
![]() $f^{-1}(\varDelta ) \in \mathscr {A}$
for all
$f^{-1}(\varDelta ) \in \mathscr {A}$
for all
![]() $\varDelta \in \mathscr {B}$
) is
$\varDelta \in \mathscr {B}$
) is
![]() $\sigma $
-surjective if the corresponding map
$\sigma $
-surjective if the corresponding map
![]() $\mathscr {B} \ni \varDelta \longmapsto f^{-1}(\varDelta ) \in \mathscr {A}$
is surjective. If
$\mathscr {B} \ni \varDelta \longmapsto f^{-1}(\varDelta ) \in \mathscr {A}$
is surjective. If
![]() $Y$
is a topological Hausdorff space,
$Y$
is a topological Hausdorff space,
![]() $\sigma $
-surjectivity refers to
$\sigma $
-surjectivity refers to
![]() $\mathscr {B}=\mathfrak {B}(Y)$
. In case
$\mathscr {B}=\mathfrak {B}(Y)$
. In case
![]() $\mathscr {A}=\mathfrak {B}(X)$
and
$\mathscr {A}=\mathfrak {B}(X)$
and
![]() $\mathscr {B}=\mathfrak {B}(Y)$
, where
$\mathscr {B}=\mathfrak {B}(Y)$
, where
![]() $X$
and
$X$
and
![]() $Y$
are topological Hausdorff spaces,
$Y$
are topological Hausdorff spaces,
![]() $\sigma $
-surjectivity is called in [Reference Cichoń, Stochel and Szafraniec15] Borel injectivity. It is worth emphasizing here that the property of being
$\sigma $
-surjectivity is called in [Reference Cichoń, Stochel and Szafraniec15] Borel injectivity. It is worth emphasizing here that the property of being
![]() $\sigma $
-surjective was used in the proof of Theorem 1.7.
$\sigma $
-surjective was used in the proof of Theorem 1.7.
Applying the measure transport theorem together with Theorems 1.3 and 1.7, we get the following.
Theorem 7.1 Assume that
![]() $(X, \mathscr {A})$
is a measurable space,
$(X, \mathscr {A})$
is a measurable space,
![]() $F\colon \mathscr {A} \to \boldsymbol {B}(\mathcal {H})$
is a semispectral measure,
$F\colon \mathscr {A} \to \boldsymbol {B}(\mathcal {H})$
is a semispectral measure,
![]() $T \in \boldsymbol {B}(\mathcal {H})$
is a self-adjoint operator, and
$T \in \boldsymbol {B}(\mathcal {H})$
is a self-adjoint operator, and
![]() $p,q$
are positive integers such that
$p,q$
are positive integers such that
![]() $p<q$
. Let
$p<q$
. Let
![]() $\omega \colon X\to \mathbb {R}$
be an
$\omega \colon X\to \mathbb {R}$
be an
![]() $F$
-essentially bounded
$F$
-essentially bounded
![]() $\sigma $
-surjective function such that
$\sigma $
-surjective function such that
If
![]() $p$
is odd and
$p$
is odd and
![]() $q$
is even, or if
$q$
is even, or if
![]() $T \geqslant 0$
and
$T \geqslant 0$
and
![]() $\omega (X) \subseteq \mathbb {R}_+$
, then
$\omega (X) \subseteq \mathbb {R}_+$
, then
![]() $F$
is a spectral measure.
$F$
is a spectral measure.
It is worth pointing out that there is a wide class of measurable spaces admitting functions
![]() $\omega $
with the properties mentioned in Theorem 7.1. Namely, if
$\omega $
with the properties mentioned in Theorem 7.1. Namely, if
![]() $X$
is a Borel subset of a complete separable metric space and
$X$
is a Borel subset of a complete separable metric space and
![]() $K$
is a bounded Borel subset of
$K$
is a bounded Borel subset of
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
![]() $X$
and
$X$
and
![]() $K$
have the same cardinality, then by [Reference Parthasarathy40, Theorem 2.12] there exists a bijection
$K$
have the same cardinality, then by [Reference Parthasarathy40, Theorem 2.12] there exists a bijection
![]() $\omega _0\colon X \to K$
such that
$\omega _0\colon X \to K$
such that
![]() $\omega _0$
and
$\omega _0$
and
![]() $\omega _0^{-1}$
are Borel measurable. This implies that the function
$\omega _0^{-1}$
are Borel measurable. This implies that the function
![]() $\omega \colon X \to \mathbb {R}$
defined by
$\omega \colon X \to \mathbb {R}$
defined by
![]() $\omega (x)=\omega _0(x)$
for
$\omega (x)=\omega _0(x)$
for
![]() $x\in X$
is bounded and
$x\in X$
is bounded and
![]() $\sigma $
-surjective. It turns out that the notions of injectivity and
$\sigma $
-surjective. It turns out that the notions of injectivity and
![]() $\sigma $
-surjectivity coincide for continuous maps
$\sigma $
-surjectivity coincide for continuous maps
![]() $f\colon X \to Y$
between topological Hausdorff spaces whenever
$f\colon X \to Y$
between topological Hausdorff spaces whenever
![]() $X$
is
$X$
is
![]() $\sigma $
-compact (see [Reference Cichoń, Stochel and Szafraniec15, Proposition 16]). Coming back to the case of
$\sigma $
-compact (see [Reference Cichoń, Stochel and Szafraniec15, Proposition 16]). Coming back to the case of
![]() $X=Y=\mathbb {R}$
, let us recall the well-known example of a bounded continuous and injective (consequently,
$X=Y=\mathbb {R}$
, let us recall the well-known example of a bounded continuous and injective (consequently,
![]() $\sigma $
-surjective) function
$\sigma $
-surjective) function
![]() $\omega \colon \mathbb {R} \to \mathbb {R}$
given by
$\omega \colon \mathbb {R} \to \mathbb {R}$
given by
![]() $\omega (x) = \frac {x}{1+|x|}$
for
$\omega (x) = \frac {x}{1+|x|}$
for
![]() $x \in \mathbb {R}$
.
$x \in \mathbb {R}$
.