Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T01:12:44.769Z Has data issue: false hasContentIssue false
  • English
  • Français

Triangles of Baumslag–Solitar Groups

Published online by Cambridge University Press:  20 November 2018

Daniel Allcock
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our main result is that many triangles of Baumslag–Solitar groups collapse to finite groups, generalizing a famous example of Hirsch and other examples due to several authors. A triangle of Baumslag–Solitar groups means a group with three generators, cyclically ordered, with each generator conjugating some power of the previous one to another power. There are six parameters, occurring in pairs, and we show that the triangle fails to be developable whenever one of the parameters divides its partner, except for a few special cases. Furthermore, under fairly general conditions, the group turns out to be finite and solvable of derived length 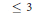$\le \,3$. We obtain a lot of information about finite quotients, even when we cannot determine developability.

Keywords

20F0620F65
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 2 , 16 April 2012 , pp. 241 - 253
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Albar, M. A. and Al-Shuaibi, A-A. A., On Mennicke groups of deficiency zero II. Canad. Math. Bull. 34(1991), 289–293. http://dx.doi.org/10.4153/CMB-1991-046-5 Google Scholar
[2] Baumslag, G. and Solitar, D. Some two-generator one-relator non-Hopfian groups. Bull. Amer. Math. Soc. 68(1962), 199–201. http://dx.doi.org/10.1090/S0002-9904-1962-10745-9 Google Scholar
[3] Bridson, M. and Haefliger, A. Metric spaces of nonpositive curvature. Grundlehren Math.Wiss. 319, Springer-Verlag, Berlin, 1999.Google Scholar
[4] Farb, B., Hruska, C. and Thomas, A., Problems on automorphism groups of nonpositively curved polyhedral complexes and their lattices. To appear in: (Farb, B. and Fisher, D., eds.) Geometry, rigidity, and group actions. A festschrift in honor of Robert Zimmer's 60th birthday. arxiv:math.GR:0803.2484.Google Scholar
[5] The GAP Group, GAP – Groups, Algorithms, and Programming, Version 4.4.10; 2007. (http://www.gap-system.org)Google Scholar
[6] Haefliger, A., Complexes of groups and orbihedra. In: Group theory from a geometrical viewpoint (Trieste, 1990), World Sci. Publ., River Edge, NJ, 1991, 504–540.Google Scholar
[7] Frédéric Haglund, Existence, unicité et homogénéité de certains immeubles hyperboliques. Math. Z. 242(2002), 97–148. http://dx.doi.org/10.1007/s002090100309 Google Scholar
[8] Higman, G., A finitely generated infinite simple group. J. London Math. Soc. 26(1951), 61–64. http://dx.doi.org/10.1112/jlms/s1-26.1.61 Google Scholar
[9] Ivanov, A. A. and Meierfrankenfeld, U., A Computer-Free Construction of J4. J. Algebra 219(1999), 113–172. http://dx.doi.org/10.1006/jabr.1999.7851 Google Scholar
[10] Jabara, E., Gruppi fattorizzati da sottogruppi ciclici. Rend. Semin. Mat. Univ. Padova 122(2009), 65–84.Google Scholar
[11] Johnson, D. L. and Robertson, E. F., Finite groups of deficiency zero. In: Homological Group Theory (Proc. Symp. Durham, 1977), London Math. Soc. Lecture Note Ser. 36, Cambridge University Press, 1979, 275–289.Google Scholar
[12] Karrass, A. and Solitar, D., Subgroups with centre in HNN groups. J. Austral. Math. Soc. Ser. A 24(1977), 350–361. http://dx.doi.org/10.1017/S1446788700020371 Google Scholar
[13] Mennicke, J., Einige endliche Gruppen mit drei Erzeugenden und drei Relationen. Arch. Math. (Basel) 10(1959), 409–418.Google Scholar
[14] Neumann, B. H., An essay on free products of groups with amalgamations. Philos. Trans. Roy. Soc. London Ser. (A) 246(1954), 503–554. http://dx.doi.org/10.1098/rsta.1954.0007 Google Scholar
[15] Neumann, B. H., Some group presentations. Canad. J. Math. 30(1978), 838–850. http://dx.doi.org/10.4153/CJM-1978-072-2 Google Scholar
[16] Post, M. J., Finite three-generator groups with zero deficiency. Comm. Algebra 6(1978), 1289–1296. http://dx.doi.org/10.1080/00927877808822292 Google Scholar
[17] Stallings, J., Non-positively curved triangles of groups. In: Group theory from a geometrical viewpoint (Trieste, 1990), World Sci. Publ., River Edge, NJ, 1991, 491–503.Google Scholar
[18] Wamsley, J. W., The deficiency of finite groups. Ph. D. thesis, Univ. of Queensland, 1969.Google Scholar
[19] Wise, D., The residual finiteness of negatively curved polygons of finite groups. Invent. Math. 149(2002), 579–617. http://dx.doi.org/10.1007/s002220200224Google Scholar