Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-11T08:35:45.860Z Has data issue: false hasContentIssue false
  • English
  • Français

Transitive Factorizations in the Hyperoctahedral Group

Published online by Cambridge University Press:  20 November 2018

G. Bini ,
I. P. Goulden  and
D. M. Jackson
G. Bini
Affiliation:
Dipartimento di Matematica, Università degli Studi di Milano, Milano, Italy e-mail: [email protected]
I. P. Goulden
Affiliation:
Department of Combinatorics and Optimization, University of Waterloo, Waterloo, ON e-mail: [email protected] e-mail: [email protected]
D. M. Jackson
Affiliation:
Department of Combinatorics and Optimization, University of Waterloo, Waterloo, ON e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The classical Hurwitz enumeration problem has a presentation in terms of transitive factorizations in the symmetric group. This presentation suggests a generalization from type 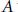$A$ to other finite reflection groups and, in particular, to type 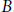$B$. We study this generalization both from a combinatorial and a geometric point of view, with the prospect of providing a means of understanding more of the structure of the moduli spaces of maps with an 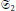${{\mathfrak{S}}_{2}}$-symmetry. The type 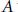$A$ case has been well studied and connects Hurwitz numbers to the moduli space of curves. We conjecture an analogous setting for the type 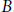$B$ case that is studied here.

Keywords

05A1514H1058D29
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 2 , 01 April 2008 , pp. 297 - 312
Copyright
Copyright © Canadian Mathematical Society 2008

References

[ELSV] Ekedahl, T., Lando, S., Shapiro, M., and Vainshtein, A., Hurwitz numbers and intersections on moduli spaces of curves. Invent.Math. 146(2001), no. 2, 297–327.Google Scholar
[F] Fulton, W., Hurwitz schemes and irreducibility of moduli of algebraic curves. Ann.Math. 90(1969), 542–575.Google Scholar
[GHJ] Goulden, I. P., Harer, J. L., and Jackson, D. M., A geometric parameterization for the virtual Euler characteristics of the moduli spaces of real and complex algebraic curves. Trans. Amer. Math. Soc. 353(2001), no. 11, 4405–4427.Google Scholar
[GJ1] Goulden, I. P. and Jackson, D. M., Transitive factorisations into transpositions and holomorphic mappings on the sphere. Proc. Amer.Math. Soc. 125(1997), no. 1, 51–60.Google Scholar
[GJ2] Goulden, I. P. and Jackson, D. M., A proof of a conjecture for the number of ramified coverings of the sphere by the torus. J. Combin. Theory Ser. A 88(1999), 246–258.Google Scholar
[GJV] Goulden, I. P., Jackson, D. M., and Vakil, R., Towards the geometry of double Hurwitz numbers. Adv. Math. 198(2005), no. 1, 43–92.Google Scholar
[Har] Harer, J., The cohomology of the moduli space of curves. In: Theory of Moduli. Lecture Notes in Math. 1337, Springer, Berlin, 1988, pp. 138–221,Google Scholar
[Hat] Hatcher, A., Algebraic Topology. Cambridge University Press, Cambridge, 2002.Google Scholar
[H] Hurwitz, A., Über Riemann’sche Flächen mit gegebenen Verzweigungspunkten. Math. Ann. 39(1891), 1–60.Google Scholar
[OP] Okounkov, A. and Pandharipande, R., Gromov-Witten theory, Hurwitz numbers, and matrix models, I. arXiv:AG-0101147.Google Scholar
[SZ] Shadrin, S. and Zvonkine, D., Changes of variables in ELSV-type formulas. Michigan Math. J. 55(2007), no. 1, 209–228.Google Scholar
[T] Tutte, W. T., Graph Theory. In: Encyclopedia of Mathematics and its Applications 21, Addison-Wesley, Reading, MA, 1984.Google Scholar
[V2] Vakil, R., Recursions for characteristic numbers of genus one plane curves. Ark. Math. 39(2001), 157–180.Google Scholar