Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:30:05.316Z Has data issue: false hasContentIssue false
  • English
  • Français

Transformations With Discrete Spectrum are Stacking Transformations

Published online by Cambridge University Press:  20 November 2018

Andrés Del Junco
Andrés Del Junco*
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

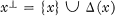The stacking method (see [1] and [5, Section 6]) has been used with great success in ergodic theory to construct a wide variety of examples of ergodic transformations (see, for example, [1 ; 3 ; 4; 5; 7]). However very little is known in general about the class of transformations which can be constructed by the stacking method using single stacks. In particular there is no simple characterization of the class .

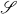Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 4 , 01 August 1976 , pp. 836 - 839
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Baxter, J. R., 4 c/a55 of ergodic automorphisms, Ph.D. Thesis, University of Toronto (1969).Google Scholar
2. Baxter, J. R., A class of ergodic transformations having simple spectrum, Proc. Amer. Math. Soc. 2Jf (1970).Google Scholar
3. Chacon, R. V., A geometric construction of measure preserving transformations, Fifth Berkeley Symposium on Probability and Statistics (2) 2 (1967), 335–360.Google Scholar
4. Chacon, R. V., Weakly mixing transformations which are not strongly mixing, Proc. Amer. Math. Soc. 22 (1969), 559–562.Google Scholar
5. Friedman, N. A., Introduction to ergodic theory (Van Nostrand Reinhold, 1970).Google Scholar
6. Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers, fourth edition (Oxford University Press 1960).Google Scholar
7. Ornstein, D. S., On the r∞t problem in ergodic theory, Proc. 6th Berkeley Symp. Math. Stat. Prob. II (Univ. of Calif. Press 1967), 347–356.Google Scholar
8. Halmos, P. R., Ergodic theory (Chelsea 1956).Google Scholar