Dans cet article, on considère un groupe semi-simple 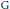$\text{G}$ classique réel et connexe. On suppose de plus que 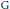$\text{G}$ possède un sous-groupe de Cartan compact. On définit une famille de sous-algèbres de Lie associée à 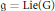$\mathfrak{g}=\text{Lie(G)}$, de même rang que g dont tous les facteurs simples sont de rang 1 ou 2. Soit 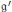$\mathfrak{g}'$ une telle sous-algèbre de Lie. On construit alors une application de transfert des intégrales orbitales de 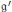$\mathfrak{g}'$ dans l’espace des intégrales orbitales de 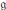$\mathfrak{g}$. On montre que cette application est définie dès que 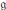$\mathfrak{g}$ ne possède pas de facteur simple réel de type CI de rang supérieur ouégal à 3. Si de plus, 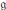$\mathfrak{g}$ ne possède pas de facteur simple de type BI de rang supérieur à 3, on montre la surjectivité de cette application de transfert.

On utilise cette application de transfert pour obtenir une formule de réduction de l’intégrale de Cauchy Harish-Chandra pour les paires duales d’algèbres de Lie réductives 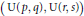$(\text{U(}p,q\text{),U(}r,s\text{)})$ et 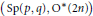$(\text{Sp(}p,q\text{),O*(2n)})$ avec 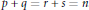$p+q=r+s=n$.