Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-25T16:55:33.073Z Has data issue: false hasContentIssue false
  • English
  • Français

Tracial oscillation zero and stable rank one

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  24 January 2024

Xuanlong Fu  and
Huaxin Lin
Xuanlong Fu
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4, Canada Current address: School of Mathematical Sciences, Tongji University, Shanghai, China e-mail: [email protected]
Huaxin Lin*
Affiliation:
Department of Mathematics, East China Normal University, Shanghai, China Current address: Department of Mathematics, University of Oregon, Eugene, OR 97403, United States
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let A be a separable (not necessarily unital) simple 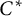$C^*$-algebra with strict comparison. We show that if A has tracial approximate oscillation zero, then A has stable rank one and the canonical map 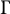$\Gamma $ from the Cuntz semigroup of A to the corresponding lower-semicontinuous affine function space is surjective. The converse also holds. As a by-product, we find that a separable simple 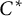$C^*$-algebra which has almost stable rank one must have stable rank one, provided it has strict comparison and the canonical map 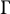$\Gamma $ is surjective.

Keywords

Tracial oscillation zerostable rank oneSimple C*-algebras

MSC classification

Primary: 46L35: Classifications of $C^*$-algebras
Secondary: 46L05: General theory of $C^*$-algebras
Type
Article
Information
Canadian Journal of Mathematics , Volume 77 , Issue 2 , April 2025 , pp. 563 - 630
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first-named author was partially supported by the Natural Sciences and Engineering Research Council of Canada Discovery Grant. The second-named author was partially supported by an NSF grant (DMS-1954600). Both authors would like to acknowledge the support during their visits to the Research Center of Operator Algebras at East China Normal University which is partially supported by Shanghai Key Laboratory of PMMP, Science and Technology Commission of Shanghai Municipality (STCSM), grant #22DZ2229014.

References

Antoine, R., Perera, F., Robert, L., and Thiel, H., ${C}^{\ast }$ -algebras of stable rank one and their Cuntz semigroups . Duke Math. J. 171(2022), 33–99.CrossRefGoogle Scholar
Blackadar, B. and Handelman, D., Dimension functions and traces on ${C}^{\ast }$ -algebra . J. Funct. Anal. 45(1982), 297–340.CrossRefGoogle Scholar
Blackadar, B. and Rørdam, M., Extending states on preordered semigroups and the existence of quasitraces on ${C}^{\ast }$ -algebras . J. Algebra 152(1992), 240–247.CrossRefGoogle Scholar
Brown, L. G., Stable isomorphism of hereditary subalgebras of $C^{\ast }$ -algebras . Pacific J. Math. 71(1977), 335–348.CrossRefGoogle Scholar
Brown, L. G. and Pedersen, G., On the geometry of the unit ball of a ${C}^{\ast }$ -algebra . J. Reine Angew. Math. 469(1995), 113–147.Google Scholar
Brown, L. G. and Pedersen, G. K., $C^{\ast }$ -algebras of real rank zero . J. Funct. Anal. 99(1991), 131–149.CrossRefGoogle Scholar
Brown, N. P., Perera, F., and Toms, A. S., The Cuntz semigroup, the Elliott conjecture, and dimension functions on $C^{\ast }$ -algebras . J. Reine Angew. Math. 621(2008), 191–211.Google Scholar
Cuntz, J., Dimension functions on simple $C^{\ast }$ -algebras . Math. Ann. 233(1978), 145–153.CrossRefGoogle Scholar
Dădărlat, M., Nagy, G., Némethi, A., and Pasnicu, C., Reduction of topological stable rank in inductive limits of $C^{\ast }$ -algebras . Pacific J. Math. 153(1992), 267–276.CrossRefGoogle Scholar
Elliott, G. A., Gong, G., Lin, H., and Niu, Z., Simple stably projectionless $C^{\ast }$ -algebras of generalized tracial rank one . J. Noncommut. Geom. 14(2020), 251–347.CrossRefGoogle Scholar
Elliott, G. A., Gong, G., Lin, H., and Niu, Z., The classification of simple separable KK-contractible $C^{\ast }$ -algebras with finite nuclear dimension . J. Geom. Phys. 158(2020), Article no. 103861, 51 pp.CrossRefGoogle Scholar
Elliott, G. A. and Niu, Z., The $C^{\ast }$ -algebra of a minimal homeomorphism of zero mean dimension . Duke Math. J. 166(2017), 3569–3594.CrossRefGoogle Scholar
Elliott, G. A., Robert, L., and Santiago, L., The cone of lower semicontinuous traces on a C*-algebra . Amer. J. Math. 133(2011), 969–1005.CrossRefGoogle Scholar
Fu, X., Li, K., and Lin, H., Tracial approximate divisibility and stable rank one . J. Lond. Math. Soc. 106(2022), 3008–3042. https://doi.org/10.1112/jlms.12654 CrossRefGoogle Scholar
Fu, X. and Lin, H., Tracial approximation in simple ${C}^{\ast }$ -algebras . Canad. J. Math. 74(2022), no. 4, 942–1004.CrossRefGoogle Scholar
Fu, X. and Lin, H., Non-amenable simple ${C}^{\ast }$ -algebras with tracial approximation . Forum Math. Sigma 10(2022), Article no. e14, 50 pp.CrossRefGoogle Scholar
Haagerup, U., Quasitraces on exact ${C}^{\ast }$ -algebras are traces . C. R. Math. Acad. Sci. Soc. R. Canada 36(2014), nos. 2–3, 67–92.Google Scholar
Kirchberg, E., On the existence of traces on exact stably projectionless simple C*-algebras . In: Operator algebras and their applications (Waterloo, ON, 1994/1995), Fields Institute Communications, 13, American Mathematical Society, Providence, RI, 1997, pp. 171–172.Google Scholar
Lin, H., Simple $C^{\ast }$ -algebras with continuous scales and simple corona algebras . Proc. Amer. Math. Soc. 112(1991), 871–880.Google Scholar
Lin, H., Approximation by normal elements with finite spectra in $C^{\ast }$ -algebras of real rank zero . Pacific J. Math. 173(1996), 443–489.CrossRefGoogle Scholar
Lin, H., Extensions by C*-algebras of real rank zero, III . Proc. Lond. Math. Soc. 76(1998), 634–666.CrossRefGoogle Scholar
Lin, H., Simple corona ${C}^{\ast }$ -algebras . Proc. Amer. Math. Soc. 132(2004), 3215–3224.CrossRefGoogle Scholar
Lin, H., Traces and simple $C^{\ast }$ -algebras with tracial topological rank zero . J. Reine Angew. Math. 568(2004), 99–137.Google Scholar
Lin, H., Local AH-algebras, Memoirs of the American Mathematical Society, 235 (1107), American Mathematical Society, Providence, RI, 2015, vi + 109. https://doi.org/10.1090/memo/1107 Google Scholar
Lin, H., Tracial oscillation zero and $\mathcal{Z}$ -stability, Adv. Math. (2021), to appear, arXiv:2112.12036.Google Scholar
Lin, H., Unitary groups and augmented Cuntz semigroups of separable simple $\mathcal{Z}$ -stable $C^{\ast }$ -algebras . Int. J. Math. 33(2022), no. 2, Article no. 2250018, 49 pp.CrossRefGoogle Scholar
Lin, H. and Zhang, S., On infinite simple $C^{\ast }$ -algebras . J. Funct. Anal. 100(1991), 221–231.CrossRefGoogle Scholar
Loring, T., Lifting solutions to perturbing problems in C*-algebras, Fields Institute Monographs, 8, American Mathematical Society, Providence, RI, 1997, x + 165.Google Scholar
Olsen, C. L. and Pedersen, G. K., Corona ${C}^{\ast }$ -algebras and their applications to lifting problems . Math. Scand. 64(1989), no. 1, 63–86.CrossRefGoogle Scholar
Pedersen, G. K., C*-algebras and their automorphism groups, London Mathematical Society Monographs, 14, Academic Press, London/New York/San Francisco, 1979.Google Scholar
Pedersen, G. K., $SA{W}^{\ast }$ -algebras and corona $C^{\ast }$ -algebras, contributions to noncommutative topology . J. Operator Theory 15(1986), 15–32.Google Scholar
Pedersen, G. K., Unitary extensions and polar decompositions in a $C^{\ast }$ -algebra . J. Operator Theory 17(1987), 357–364.Google Scholar
Pedersen, G. K., Three quavers on unitary elements in $C^{\ast }$ -algebras . Pacific J. Math. 137(1989), 169–179.CrossRefGoogle Scholar
Phillips, N. C., Large subalgebras. Preprint, 2014, arXiv:1408.5546v1.Google Scholar
Putnam, I. F., The invertible elements are dense in the irrational rotation $C^{\ast }$ -algebras . J. Reine Angew. Math. 410(1990), 160–166.Google Scholar
Rieffel, M., Dimension and stable rank in the K-theory of $C^{\ast }$ -algebras . Proc. Lond. Math. Soc. 46(1983), 301–333.CrossRefGoogle Scholar
Robert, L., Classification of inductive limits of 1-dimensional NCCW complexes . Adv. Math. 231(2012), 2802–2836.CrossRefGoogle Scholar
Robert, L., Remarks on $\mathcal{Z}$ -stable projectionless ${C}^{\ast }$ -algebras . Glasg. Math. J. 58(2016), no. 2, 273–277.CrossRefGoogle Scholar
Rørdam, M., On the structure of simple ${C}^{\ast }$ -algebras tensored with a UHF-algebra . J. Funct. Anal. 100(1991), 1–17.CrossRefGoogle Scholar
Rørdam, M., On the structure of simple ${C}^{\ast }$ -algebras tensored with a UHF-algebra. II . J. Funct. Anal. 107(1992), 255–269.CrossRefGoogle Scholar
Rørdam, M., The stable and the real rank of $\mathcal{Z}$ -absorbing ${C}^{\ast }$ -algebras . Int. J. Math. 15(2004), no. 10, 1065–1084.CrossRefGoogle Scholar
Thiel, H., Ranks of operators in simple $C^{\ast }$ -algebras with stable rank one . Commun. Math. Phys. 377(2020), 37–76.CrossRefGoogle Scholar
Tikuisis, A., Nuclear dimension, $\mathcal{Z}$ -stability, and algebraic simplicity for stably projectionless C*-algebras . Math. Ann. 358(2014), nos. 3–4, 729–778.CrossRefGoogle Scholar
Toms, A. and Winter, W., Strongly self-absorbing $C^{\ast }$ -algebras . Trans. Amer. Math. Soc. 359(2007), 3999–4029.CrossRefGoogle Scholar
Winter, W. and Zacharias, J., Completely positive maps of order zero . Münster J. Math. 2(2009), 311–324.Google Scholar
Winter, W. and Zacharias, J., The nuclear dimension of ${C}^{\ast }$ -algebras . Adv. Math. 224(2010), 461–498.CrossRefGoogle Scholar
Zhang, S., $C^{\ast }$ -algebras with real rank zero and the internal structure of their corona and multiplier algebras. III . Canad. J. Math. 42(1990), 159–190.CrossRefGoogle Scholar
Zhang, S., Matricial structure and homotopy type of simple $C^{\ast }$ -algebras with real rank zero . J. Operator Theory 26(1991), 283–312.Google Scholar