Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T15:54:11.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Torsions and intersection forms of 4-manifolds from trisection diagrams

Part of: Low-dimensional topology PL-topology

Published online by Cambridge University Press:  14 December 2020

Vincent Florens  and
Delphine Moussard
Vincent Florens*
Affiliation:
Université de Pau, Pau, Laboratoire LMAP, France e-mail: [email protected]
Delphine Moussard
Affiliation:
Université d’Aix-Marseille, I2M, Marseille, France
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Gay and Kirby introduced trisections, which describe any closed, oriented, smooth 4-manifold X as a union of three 4-dimensional handlebodies. A trisection is encoded in a diagram, namely three collections of curves in a closed oriented surface 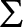$\Sigma $ , guiding the gluing of the handlebodies. Any morphism 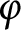$\varphi $ from 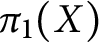$\pi _1(X)$ to a finitely generated free abelian group induces a morphism on 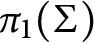$\pi _1(\Sigma )$ . We express the twisted homology and Reidemeister torsion of 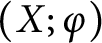$(X;\varphi )$ in terms of the first homology of 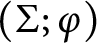$(\Sigma ;\varphi )$ and the three subspaces generated by the collections of curves. 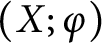We also express the intersection form of $(X;\varphi )$ in terms of the intersection form of 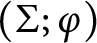$(\Sigma ;\varphi )$ .

Keywords

4-manifold trisectionsintersection formsReidemeister torsion

MSC classification

Primary: 57Q10: Simple homotopy type, Whitehead torsion, Reidemeister-Franz torsion, etc.
Secondary: 57M99: None of the above, but in this section
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 2 , April 2022 , pp. 527 - 549
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was partially supported by the ANR Project LISA 17-CE40-0023-01. While working on the contents of this paper, the second author has been supported by a Postdoctoral Fellowship of the Japan Society for the Promotion of Science. She is grateful to Tomotada Ohtsuki and the Research Institute for Mathematical Sciences for their support. She is now supported by the Région Bourgogne Franche-Comté project ITIQ–3D. She thanks Gwénaël Massuyeau and the Institut de Mathématiques de Bourgogne for their support.

References

Blanchfield, R. C., Intersection theory of manifolds with operators with applications to knot theory . Ann. Math. Second Series 65(1957), 340–356.CrossRefGoogle Scholar
Feller, P., Klug, M., Schirmer, T., and Zemke, D., Calculating the homology and intersection form of a $4$ -manifold from a trisection diagram. Proc. Natl. Acad. Sci. U.S.A. 115(2018), no. 43, 10869–10874. http://doi.org/10.1073/pnas.1717176115 CrossRefGoogle ScholarPubMed
Gay, D. and Kirby, R., Trisecting 4-manifolds . Geom. Topol. 20(2016), no. 6, 3097–3132.CrossRefGoogle Scholar
Kirk, P. and Livingston, C., Twisted Alexander invariants, Reidemeister torsion, and Casson–Gordon invariants . Topology. 38(1999), no. 3, 635–661.CrossRefGoogle Scholar
Koenig, D., Trisections of 3-manifold bundles over S1 . Preprint, 2017. arxiv:1710.04345 Google Scholar
Laudenbach, F. and Poénaru, V., A note on 4-dimensional handlebodies . Bull. Soc. Math. France 100(1972), 337–344.CrossRefGoogle Scholar
Milnor, J., Whitehead torsion . Bull. Amer. Math. Soc. 72(1966), 358–426.CrossRefGoogle Scholar
Ranicki, A., The Maslov index and the Wall signature non-additivity invariant. Unpublished, 1997. https://www.maths.ed.ac.uk/~v1ranick/papers/maslov.pdf Google Scholar
Reidemeister, K., Durchschnitt und Schnitt von Homotopieketten. Monatshefte für Mathematik und Physik 48 (1939), pp. 226–239.Google Scholar
Turaev, V., Introduction to combinatorial torsions. In Notes taken by Felix Schlenk, Lectures in Mathematics ETH Zürich, Birkhäuser Verlag, Basel, 2001.CrossRefGoogle Scholar
Wall, C. T. C., Non-additivity of the signature . Invent. Math. 7(1969), 269–274.CrossRefGoogle Scholar