Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-24T11:39:31.428Z Has data issue: false hasContentIssue false
  • English
  • Français

Torsion in the space of commuting elements in a Lie group

Part of: Homotopy theory

Published online by Cambridge University Press:  22 May 2023

Daisuke Kishimoto Open the ORCID record for Daisuke Kishimoto [Opens in a new window]  and
Masahiro Takeda
Daisuke Kishimoto
Affiliation:
Faculty of Mathematics, Kyushu University, Fukuoka 819-0395, Japan e-mail: [email protected]
Masahiro Takeda*
Affiliation:
Institute for Liberal Arts and Sciences, Kyoto University, Kyoto 606-8316, Japan
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a compact connected Lie group, and let 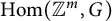$\operatorname {Hom}({\mathbb {Z}}^m,G)$ be the space of pairwise commuting m-tuples in G. We study the problem of which primes $p \operatorname {Hom}({\mathbb {Z}}^m,G)_1$, the connected component of 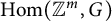$\operatorname {Hom}({\mathbb {Z}}^m,G)$ containing the element $(1,\ldots ,1)$, has p-torsion in homology. We will prove that 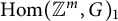$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$ for 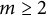$m\ge 2$ has p-torsion in homology if and only if p divides the order of the Weyl group of G for 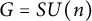$G=SU(n)$ and some exceptional groups. We will also compute the top homology of 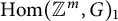$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$ and show that $\operatorname {Hom}({\mathbb {Z}}^m,G)_1$ always has 2-torsion in homology whenever G is simply-connected and simple. Our computation is based on a new homotopy decomposition of 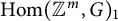$\operatorname {Hom}({\mathbb {Z}}^m,G)_1$, which is of independent interest and enables us to connect torsion in homology to the combinatorics of the Weyl group.

Keywords

Space of commuting elementsLie groupWeyl grouphomotopy colimitBousfield–Kan spectral sequenceextended Dynkin diagram

MSC classification

Primary: 57S05: Topological properties of groups of homeomorphisms or diffeomorphisms 55P65: Homotopy functors
Type
Article
Information
Canadian Journal of Mathematics , Volume 76 , Issue 3 , June 2024 , pp. 1033 - 1061
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author was supported by JSPS KAKENHI (Grant Nos. JP17K05248 and JP19K03473), and the second author was supported by JSPS KAKENHI (Grant No. JP21J10117).

References

Adem, A. and Cohen, F. R., Commuting elements and spaces of homomorphisms . Math. Ann. 338(2007), 587–626.CrossRefGoogle Scholar
Adem, A., Cohen, F. R., and Torres-Giese, E., Commuting elements, simplicial spaces, and filtrations of classifying spaces . Math. Proc. Cambridge Philos. Soc. 152(2012), no. 1, 91–114.CrossRefGoogle Scholar
Adem, A., Gómez, J. M., and Gritschacher, S., On the second homotopy group of spaces of commuting elements in Lie groups . Int. Math. Res. Not. 2022(2022), 1–73.CrossRefGoogle Scholar
Atiyah, M. F. and Bott, R., The Yang–Mills equations over Riemann surfaces . Philos. Trans. R. Soc. Lond. Ser. A 308(1983), no. 1505, 523–615.Google Scholar
Baird, T., Jeffrey, L. C., and Selick, P., The space of commuting $n$ -tuples in $SU(2)$ . Illinois J. Math. 55(2011), no. 3, 805–813.CrossRefGoogle Scholar
Baird, T. J., Cohomology of the space of commuting $n$ -tuples in a compact Lie group . Algebr. Geom. Topol. 7(2007), 737–754.CrossRefGoogle Scholar
Bergeron, M., The topology of nilpotent representations in reductive groups and their maximal compact subgroups . Geome. Topol. 19(2015), no. 3, 1383–1407.CrossRefGoogle Scholar
Bergeron, M. and Silberman, L., A note on nilpotent representations . J. Group Theory 19(2016), no. 1, 125–135.CrossRefGoogle Scholar
Borel, A., Sous-groupes commutatifs et torsion des groupes de Lie compactes . Tôhoku Math. J. 13(1962), 216–240.Google Scholar
Borel, A., Friedman, R., and Morgan, J., Almost commuting elements in compact Lie groups . Mem. Amer. Math. Soc. 157(2002), 747.Google Scholar
Bousfield, A. K. and Kan, D. M., Homotopy limits, completions and localizations, Lecture Notes in Mathematics, 304, Springer, Berlin, 1972.CrossRefGoogle Scholar
Bredon, G. E., Introduction to compact transformation groups, Pure and Applied Mathematics, 46, Academic Press, New York, 1972.Google Scholar
Crabb, M. C., Spaces of commuting elements in $SU(2)$ , Proc. Edinb. Math. Soc. 54(2011), 67–75.CrossRefGoogle Scholar
Culler, M. and Shalen, P. B., Varieties of group representations and splittings of 3-manifolds . Ann. of Math. (2) 117(1983), no. 1, 109–146.CrossRefGoogle Scholar
Goldman, W. M., Topological components of spaces of representations . Invent. Math. 93(1988), no. 3, 557–607.CrossRefGoogle Scholar
Gómez, J. M., Pettet, A., and Souto, J., On the fundamental group of $Hom\left({\mathbb{Z}}^k,G\right)$ . Math. Z. 271(2012), 33–44.CrossRefGoogle Scholar
Hasui, S., Kishimoto, D., Takeda, M., and Tsutaya, M., Tverberg’s theorem for cell complexes . accepted by Bull. Lond. Math. Soc. (2023).CrossRefGoogle Scholar
Hitchin, N. J., The self-duality equations on a Riemann surface . Proc. Lond. Math. Soc. (3) 55(1987), no. 1, 59–126.CrossRefGoogle Scholar
Humphreys, J. E., Reflection groups and coxeter groups, Cambridge Studies in Advanced Mathematics, 29, Cambridge University Press, Cambridge, 1990.CrossRefGoogle Scholar
Kac, V. G. and Smilga, A. V., Vacuum structure in supersymmetric Yang–Mills theories with any gauge group . In: The many faces of the superworld, edited by M Shifman (University of Minne sota) World Scientific Publishing, River Edge, NJ, 1999, pp. 185–234.Google Scholar
Kishimoto, D. and Takeda, M., Spaces of commuting elements in the classical groups . Adv. Math. 386(2021), 107809.CrossRefGoogle Scholar
Kozlov, D., Combinatorial algebraic topology, Algorithms and Computation in Mathematics, 21, Springer, Berlin, 2008.CrossRefGoogle Scholar
Mimura, M. and Toda, H., Topology of Lie groups I, II, Translations of Mathematical Monographs, 91, American Mathematical Society, Providence, RI, 1991.Google Scholar
Ramras, D. A. and Stafa, M., Hilbert–Poincaré series for spaces of commuting elements in Lie groups . Math. Z. 292(2019), 591–610.CrossRefGoogle Scholar
Ramras, D. A. and Stafa, M., Homological stability for spaces of commuting elements in Lie groups . Int. Math. Res. Not. 2021(2021), no. 5, 3927–4002.CrossRefGoogle Scholar
Takeda, M., Cohomology of the spaces of commuting elements in Lie groups of rank two . Topology Appl. 303(2021), 107851.CrossRefGoogle Scholar
Wehrheim, K., Uhlenbeck compactness, EMS Series of Lectures in Mathematics, European Mathematical Society, Zürich, 2004.CrossRefGoogle Scholar
Witten, E., Constraints on supersymmetry breaking . Nuclear Phys. B 202(1982), 253–316.CrossRefGoogle Scholar
Witten, E., Toroidal compactification without vector structure . J. High Energy Phys. 6(1998), 43 pp.Google Scholar