Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T01:17:42.319Z Has data issue: false hasContentIssue false
  • English
  • Français

Topology of Gleason Parts in Maximal Ideal Spaces with no Analytic Discs

Part of: Holomorphic functions of several complex variables Commutative Banach algebras and commutative topological algebras Holomorphic convexity

Published online by Cambridge University Press:  15 November 2019

Alexander J. Izzo  and
Dimitris Papathanasiou
Alexander J. Izzo
Affiliation:
Department of Mathematics and Statistics, Bowling Green State University, Bowling Green, OH 43403 Email: [email protected]
Dimitris Papathanasiou
Affiliation:
Laboratoire de Mathématiques, Université Blaise Pascal, Campus des Cézeaux, F-63177 Aubiere Cedex, France Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We strengthen, in various directions, the theorem of Garnett that every $\unicode[STIX]{x1D70E}$-compact, completely regular space 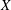$X$ occurs as a Gleason part for some uniform algebra. In particular, we show that the uniform algebra can always be chosen so that its maximal ideal space contains no analytic discs. We show that when the space 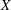$X$ is metrizable, the uniform algebra can be chosen so that its maximal ideal space is metrizable as well. We also show that for every locally compact subspace 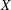$X$ of a Euclidean space, there is a compact set 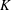$K$ in some 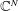$\mathbb{C}^{N}$ so that 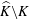$\widehat{K}\backslash K$ contains a Gleason part homeomorphic to 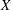$X$, and 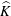$\widehat{K}$ contains no analytic discs.

MSC classification

Primary: 46J10: Banach algebras of continuous functions, function algebras
Secondary: 46J15: Banach algebras of differentiable or analytic functions, $H^p$-spaces 32A65: Banach algebra techniques 32E20: Polynomial convexity
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 1 , February 2021 , pp. 177 - 194
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Author A.I. was partially supported by a Simons collaboration grant and by NSF Grant DMS-1856010. Author D.P. was supported by the Fonds de la Recherche Scienti que-FNRS, grant no. PDR T.0164.16

References

Basener, R. F., On rationally convex hulls. Trans. Amer. Math. Soc. 182(1973), 353–381. https://doi.org/10.2307/1996538CrossRefGoogle Scholar
Browder, A., Introduction to function algebras. W. A. Benjamin, Inc., New York-Amsterdam, 1969.Google Scholar
Cole, B. J., One-point parts and the peak point conjecture. Ph.D. dissertation, Yale University, 1968.Google Scholar
Cole, B. J., Ghosh, S. N., and Izzo, A. J., A hull with no nontrivial Gleason parts. Indiana Univ. Math. J. 67(2018), 739–752. https://doi.org/10.1512/iumj.2018.67.7300CrossRefGoogle Scholar
Dales, H. G. and Feinstein, J. F., Banach function algebras with dense invertible group. Proc. Amer. Math. Soc. 136(2008), 1295–1304. https://doi.org/10.1090/S0002-9939-07-09044-2CrossRefGoogle Scholar
Feinstein, J. F., A nontrivial strongly regular uniform algebra. J. London Math. Soc. 45(1992), 288–300. https://doi.org/10.1112/jlms/s2-45.2.288CrossRefGoogle Scholar
Feinstein, J. F., Regularity conditions for Banach function algebras. In: Function spaces (Edwardsville, IL, 1994). Lecture Notes in Pure and Applied Math., 172, Dekker, New York, 1995, pp. 117–122.Google Scholar
Feinstein, J. F., A counterexample to a conjecture of S. E. Morris. Proc. Amer. Math. Soc. 132(2004), 2389–2397. https://doi.org/10.1090/S0002-9939-04-07382-4CrossRefGoogle Scholar
Feinstein, J. F. and Heath, M. J., Regularity and amenability conditions for uniform algebras. In: Function spaces. Contemp. Math., 435, Amer. Math. Soc., Providence, RI, 2007, pp. 159–169. https://doi.org/10.1090/conm/435/08374CrossRefGoogle Scholar
Feinstein, J. F. and Izzo, A. J., A general method for constructing essential uniform algebras. Studia Math. 246(2019), 47–61. https://doi.org/10.4064/sm170907-23-2CrossRefGoogle Scholar
Gamelin, T. W. and Rossi, H., Jensen measures and algebras of analytic functions. In: 1966 Function algebras (Proc. Internat. Sympos. on Function Algebras, Tulane Univ., 1965). Scott-Foresman, Chicago, Ill., 1966, pp. 15–35.Google Scholar
Garnett, J., A topological characterization of Gleason parts. Pacific J. Math. 20(1967), 59–63.10.2140/pjm.1967.20.59CrossRefGoogle Scholar
Gleason, A., Function algebras. Seminar on Analytic Functions, vol. II, Institute for Advanced Study, Princeton, 1957, pp. 213–226.Google Scholar
Hurewicz, W. and Wallman, H., Dimension theory. Revised ed.Princeton University Press, Princeton, NJ, 1948.Google Scholar
Izzo, A. J., Gleason parts and point derivations for uniform algebras with dense invertible group. Trans. Amer. Math. Soc. 370(2018), 4299–4321. https://doi.org/10.1090/tran/7153CrossRefGoogle Scholar
Izzo, A. J., Spaces with polynomial hulls that contain no analytic discs. Math. Ann., to appear.Google Scholar
Izzo, A. J., A doubly generated uniform algebra with a one-point Gleason part off its Shilov boundary. Studia Math. 252(2020), 311–319.10.4064/sm190224-7-6CrossRefGoogle Scholar
Izzo, A. J., Gleason parts and point derivations for uniform algebras with dense invertible group II. arxiv:1910.11705Google Scholar
Jameson, G. J. O., Topology and normed spaces. Chapman and Hall, London, 1974.Google Scholar
Rossi, H., Holomorphically convex sets in several complex variables. Ann. of Math. 74(1961), 470–493. https://doi.org/10.2307/1970292CrossRefGoogle Scholar
Stolzenberg, G., A hull with no analytic structure. J. Math. Mech. 12(1963), 103–111.Google Scholar
Stout, E. L., The theory of uniform algebras. Bogden & Quigley, New York, 1971.Google Scholar