Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T01:17:14.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Topologizing Different Classes of Real Functions

Published online by Cambridge University Press:  20 November 2018

Krzysztof Ciesielski
Krzysztof Ciesielski*
Affiliation:
Department of Mathematics, West Virginia University Morgantown, West Virginia 26506-6310, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this paper is to examine which classes 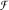of functions from 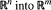can be topologized in a sense that there exist topologies τ1 and τ2 on 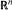and 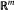respectively, such that 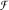is equal to the class C(τ1 , τ2) of all continuous functions 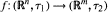. We will show that the Generalized Continuum Hypothesis GCH implies the positive answer for this question for a large number of classes of functions 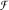for which the sets {x : f(x) = g(x)} are small in some sense for all f, g ∈ 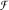f ≠ g. The topologies will be Hausdorff and connected. It will be also shown that in some model of set theory ZFC with GCH these topologies could be completely regular and Baire. One of the corollaries of this theorem is that GCH implies the existence of a connected Hausdorff topology T on such that the class L of all linear functions g(x) = ax + b coincides with 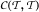. This gives an affirmative answer to a question of Sam Nadler. The above corollary remains true for the class of all polynomials, the class of all analytic functions and the class of all harmonic functions.

We will also prove that several other classes of real functions cannot be topologized. This includes the classes of C∞ functions, differentiable functions, Darboux functions and derivatives.

Keywords

26A1554H1003E35topologies on Rnlinearanalytic and harmonic functionsderivatives
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 6 , 01 December 1994 , pp. 1188 - 1207
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Bruckner, A. M., Differentiation of Real Functions, Lecture Notes in Math. 659, Springer-Verlag, 1978.Google Scholar
2. Chazarain, Jacques and Piriou, Alain, Introduction to the Theory of Linear Partial Differential Equations, North-Holland, 1982.Google Scholar
3. Ciesielski, Krzysztof, Linear subspaces of without dense totally disconnected subset, Fund. Math. 142(1993), 85–88.Google Scholar
3a. Ciesielski, Krzysztof and Larson, Lee, Various continuities with the density, I-density and ordinary topologies on R, Real Anal. Exchange 17(1991-92), 183–210.Google Scholar
5. Ciesielski, Krzysztof and Larson, Lee and Krzysztof Ostaszewski, I-density continuous functions, Mem. Amer. Math. Soc. (515), 107, 1994.Google Scholar
6. Denjoy, A., Mémoire sur les dérivés des fonctions continues, J. Math. Pures et Appl. 1(1915), 105–240.Google Scholar
7. Engelking, Ryszard, General Topology, Warszawa, 1977.Google Scholar
8. Goffman, C. and Neugebauer, C. J. and Nishiura, T., The Density Topology and Approximate Continuity, Duke Math. J. 28(1961), 497–506.Google Scholar
9. Goffman, Casper and Waterman, Daniel, Approximately Continuous Transformations, Proc. Amer. Math. Soc. 12(1961), 116–121.Google Scholar
10. Haupt, O. and Pauc, Ch., La topologie de Denjoy envisagée comme vraie topologie, C. R. Acad. Sci. Paris 234(1952), 390–392.Google Scholar
11. Kunen, K., Set Theory, North-Holland, 1983.Google Scholar
12. Miller, A. W., The Baire category theorem and cardinals of countable cofinality, J. Symbolic Logic 47(1982), 275–288.Google Scholar
13. Oxtoby, J. C., Measure and Category, Springer-Verlag, 1971.Google Scholar
14. Wilczyriski, W., A category analogue of the density topology, approximate continuity, and the approximate derivative, Real Anal. Exchange 10(1984-85), 241–265.Google Scholar
15. Zahorski, Z., Sur la Premiere Dérivée, Trans. Amer. Math. Soc. 69(1950), 1–54.Google Scholar