Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T06:19:44.328Z Has data issue: false hasContentIssue false
  • English
  • Français

Topologically Versal Deformations of Matrices; Codimension at most Two

Published online by Cambridge University Press:  20 November 2018

D. W. Bass
D. W. Bass*
Affiliation:
Memorial University, St. John's, Newfoundland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. The reduction of a matrix to its Jordan normal form is an unstable operation in that both the normal form itself and the reducing mapping depend discontinuously on the elements of the original matrix. For example, the matrix 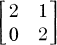trivially reduces to itself in Jordan form, but there are arbitrarily small perturbations of this matrix that reduce to the form 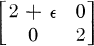which is certainly not a small perturbation of the original matrix, and moreover the reducing mapping is not a small perturbation of the identity. In [1], Arnol'd derives the simplest possible normal forms to which families of matrices may be linearly reduced in a ‘stable’ manner. In this paper, we consider a ‘topological' version of the problem, using the classification of matrices up to topological conjugacy given in [8] and the classification of linear dynamical systems up to orbital equivalence given in [9].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 1 , 01 February 1981 , pp. 168 - 180
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Arnol'd, V. I., On matrices depending on parameters, Russian Math. Surveys 26 (1971), 29–43.Google Scholar
2. Arnol'd, V. I., Lectures on bifurcations and versai families, Russian Math. Surveys 27 (1972), 54–123.Google Scholar
3. Bass, D. W., Topological classification of endomorphisms of real line bundles, J. Lond. Math. Soc. 19 (1979), 143–151.Google Scholar
4. Bass, D. W., Topological classification of endormorphisms of complex line bundles, J. Lond. Math. Soc. 19 (1979) 152–160.Google Scholar
5. Bass, D. W., Topologically versai deformations of matrices: codimension at most one, J. Lond. Math. Soc. 16 (1977), 553–558.Google Scholar
6. Cappell, S. E. and Shaneson, J. L., Non linear similarity of matrices, Bull. Amer. Math. Soc, Vol. 1(6) Nov. (1979), 899–902.Google Scholar
7. Galin, D. M.. On real matrices depending on parameters, Uspekhi Mat. Nauk. 27 (1972), 241–242.Google Scholar
8. Kuiper, N. and Robbin, J. W., Topological classification of linear endomorphisms, Invent. Math. 19 (1973), 83–106.Google Scholar
9. Kuiper, N., The topology of the solutions of a linear differential equation on Rn, Diff. Geom. (Proc. Sympos. Pure Math. 27 Part 1, Stanford University, Stanford, California, 1973).Google Scholar
10. Robbin, J. W., Topological conjugacy and structural stability for discrete dynamical systems, Bull. Amer. Math. Soc. 75(b) (1972), 923–952.Google Scholar