Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gardner, R. J.
1982.
Measure Theory Oberwolfach 1981.
Vol. 945,
Issue. ,
p.
42.
1987.
Saks Spaces and Applications to Functional Analysis.
Vol. 139,
Issue. ,
p.
106.


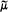 on the product space
on the product space 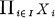 , then considering the restriction to the inverse limit set
, then considering the restriction to the inverse limit set 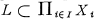 .
.