Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-13T19:36:02.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological Free Entropy Dimensions in Nuclear C*-algebras and in Full Free Products of Unital C*-algebras

Published online by Cambridge University Press:  20 November 2018

Don Hadwin ,
Qihui Li  and
Junhao Shen
Don Hadwin
Affiliation:
Department of Mathematics and Statistics, University of New Hampshire, Durham, NH 03824, U.S.A. email: [email protected]@[email protected]
Qihui Li
Affiliation:
Department of Mathematics and Statistics, University of New Hampshire, Durham, NH 03824, U.S.A. email: [email protected]@[email protected]
Junhao Shen
Affiliation:
Department of Mathematics and Statistics, University of New Hampshire, Durham, NH 03824, U.S.A. email: [email protected]@[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the paper, we introduce a new concept, topological orbit dimension of an $n$-tuple of elements in a unital 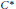${{\text{C}}^{*}}$-algebra. Using this concept, we conclude that Voiculescu's topological free entropy dimension of every finite family of self-adjoint generators of a nuclear 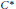${{\text{C}}^{*}}$-algebra is less than or equal to 1. We also show that the Voiculescu's topological free entropy dimension is additive in the full free product of some unital 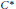${{\text{C}}^{*}}$-algebras. We show that the unital full free product of Blackadar and Kirchberg's unital 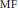$\text{MF}$ algebras is also an 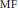$\text{MF}$ algebra. As an application, we obtain that 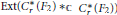$\text{Ext(}C_{r}^{*}\text{(}{{F}_{2}}\text{)}{{\text{*}}_{\mathbb{C}}}C_{r}^{*}\text{(}{{F}_{2}}\text{))}$ is not a group.

Keywords

46L1046L54topological free entropy dimensionunital C*-algebra
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 3 , 01 June 2011 , pp. 551 - 590
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Blackadar, B. and Kirchberg, E., Generalized inductive limits of finite-dimensional C*-algebras. Math. Ann. 307(1997), no. 3, 343–380. doi:10.1007/s002080050039 Google Scholar
[2] Blackadar, B., Kumjian, A., and Rørdam, M., Approximately central matrix units and the structure of noncommutative tori. K-Theory 6(1992), no. 3, 267–284. doi:10.1007/BF00961466 Google Scholar
[3] Boca, F. P., A note on full free product C*-algebras, lifting and quasidiagonality. In: Operator theory, operator algebras and related topics (Timişoara, 1996), Theta Found., Bucharest, 1997, pp. 51–63.Google Scholar
[4] Brown, N. P., On quasidiagonal C*-algebras. In: Operator algebras and applications, Adv. Stud. Pure Math., 38, Math. Soc. Japan, Tokyo, 2004, pp. 19–64.Google Scholar
[5] Brown, N. P., Dykema, K., and Jung, K., Free entropy dimension in amalgamated free products. Proc. Lond. Math. Soc. 97(2008), no. 2, 339–369. doi:10.1112/plms/pdm054 Google Scholar
[6] Choi, M. D., The full C*-algebra of the free group on two generators. Pacific J. Math. 87(1980), no. 1, 41–48.Google Scholar
[7] Dykema, K., Two applications of free entropy. Math. Ann. 308(1997), no. 3, 547–558. doi:10.1007/s002080050088 Google Scholar
[8] Exel, R. and Loring, T. A., Finite-dimensional representations of free product C*-algebras. Internat. J. Math. 3(1992), no. 4, 469–476. doi:10.1142/S0129167X92000217 Google Scholar
[9] Ge, L., Applications of free entropy to finite von Neumann algebras. Amer. J. Math. 119(1997), no. 2, 467–485. doi:10.1353/ajm.1997.0012 Google Scholar
[10] Ge, L., Applications of free entropy to finite von Neumann algebras. II. Ann. of Math. (2) 147(1998), no. 1, 143–157. doi:10.2307/120985 Google Scholar
[11] Ge, L. and Hadwin, D., Ultraproducts of C*-algebras. In: Recent advances in operator theory and related topics (Szeged, 1999), Oper. Theory Adv. Appl., 127, Birkhäuser, Basel, 2001, pp. 305–326.Google Scholar
[12] Ge, L. and Popa, S., On some decomposition properties for factors of type II1. Duke Math. J. 94(1998), no. 1, 79–101. doi:10.1215/S0012-7094-98-09405-4 Google Scholar
[13] Ge, L. and Shen, J., Free entropy and property T factors. Proc. Natl. Acad. Sci. USA 97(2000), no. 18, 9881–9885 (electronic). doi:10.1073/pnas.97.18.9881 Google Scholar
[14] Ge, L. and Shen, J., On free entropy dimension of finite von Neumann algebras. Geom. Funct. Anal. 12(2002), no. 3, 546–566. doi:10.1007/s00039-002-8256-6 Google Scholar
[15] Haagerup, U., S. Thorbjørnsen, A new application of random matrices: Ext(C¤ red(F2)) is not a group. Ann. of Math. (2) 162(2005), no. 2, 711–775. doi:10.4007/annals.2005.162.711Google Scholar
[16] Hadwin, D., Nonseparable approximate equivalence. Trans. Amer. Math. Soc. 266(1981), no. 1, 203–231. doi:10.1090/S0002-9947-1981-0613792-6 Google Scholar
[17] Hadwin, D. and Shen, J., Free orbit dimension of finite von Neumann algebras. J. Funct. Anal. 249(2007), no. 1, 75–91. doi:10.1016/j.jfa.2007.04.008 Google Scholar
[18] Hadwin, D. and Shen, J., Topological free entropy dimension in unital C¤-algebras. J. Funct. Anal. 256(2009), no. 7, 2027–2068. doi:10.1016/j.jfa.2009.01.033 Google Scholar
[19] Hadwin, D. and Shen, J., Topological free entropy dimension in unital C¤-algebras II: Orthogonal sum of unital C¤-algebras. arXiv:0708.0168v4 [math.OA]. doi:10.1016/j.jfa.2009.01.033 Google Scholar
[20] Hadwin, D. and Shen, J., Some examples of Blackadar and Kirchberg's MF algebras. arXiv:0806.4712v4 [math.OA].Google Scholar
[21] Jung, K., Strongly 1-bounded von Neumann algebras. Geom. Funct. Anal. 17(2007), no. 4, 1180–1200. doi:10.1007/s00039-007-0624-9 Google Scholar
[22] Jung, K. and Shlyakhtenko, D., Any generating set of an arbitrary property T von Neumann algebra has free entropy dimension · 1. J. Noncommut. Geom. 1(2007), no. 2, 271–279. doi:10.4171/JNCG/7 Google Scholar
[23] Szarek, S., Metric entropy of homogeneous spaces. In: Quantum probability, Banach Center Publ., 43, Polish Acad. Sci., Warsaw, 1998, pp. 395–410.Google Scholar
[24] Voiculescu, D., A non-commutative Weyl-von Neumann theorem. Rev. Roumaine Math. Pures Appl. 21(1976), no. 1, 97–113.Google Scholar
[25] Voiculescu, D., A note on quasi-diagonal C*-algebras and homotopy. Duke Math. J. 62(1991), no. 2, 267–271. doi:10.1215/S0012-7094-91-06211-3 Google Scholar
[26] Voiculescu, D., The analogues of entropy and of Fisher's information measure in free probability theory. II. Invent. Math. 118(1994), no. 3, 411–440. doi:10.1007/BF01231539 Google Scholar
[27] Voiculescu, D., The analogues of entropy and of Fisher's information measure in free probability theory. III. The absence of Cartan subalgebras. Geom. Funct. Anal. 6(1996), no. 1, 172–199. doi:10.1007/BF02246772 Google Scholar
[28] Voiculescu, D., Free entropy dimension · 1 for some generators of property T factors of type II1. J. Reine Angew. Math. 514(1999), 113–118.Google Scholar
[29] Voiculescu, D., The topological version of free entropy. Lett. Math. Phys. 62(2002), no. 1, 71–82. doi:10.1023/A:1021650130162 Google Scholar