Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Olin, Robert F.
and
Thomson, James E.
1982.
Algebras generated by a subnormal operator.
Transactions of the American Mathematical Society,
Vol. 271,
Issue. 1,
p.
299.
Yamada, Akira
1983.
A remark on the image of the Ahlfors function.
Proceedings of the American Mathematical Society,
Vol. 88,
Issue. 4,
p.
639.
Seddighi, Karim
1983.
Essential spectra of operators in the class ℬ_{𝓃}(Ω).
Proceedings of the American Mathematical Society,
Vol. 87,
Issue. 3,
p.
453.
Curto, Raul E
and
Muhly, Paul S
1985.
C∗-algebras of multiplication operators on Bergman spaces.
Journal of Functional Analysis,
Vol. 64,
Issue. 3,
p.
315.
Keren, Yan
1986.
Some properties of bergman operators.
Acta Mathematica Sinica,
Vol. 2,
Issue. 4,
p.
332.
Zhu, Ke He
1987.
VMO, ESV, and Toeplitz operators on the Bergman space.
Transactions of the American Mathematical Society,
Vol. 302,
Issue. 2,
p.
617.
Conway, John B.
1987.
Spectral properties of certain operators on Hardy spaces of planar regions.
Integral Equations and Operator Theory,
Vol. 10,
Issue. 5,
p.
659.
McGuire, Paul
1988.
C∗-algebras generated by subnormal operators.
Journal of Functional Analysis,
Vol. 79,
Issue. 2,
p.
423.
Smith, R. C.
1988.
Toeplitz operators on abstract Hardy spaces.
Glasgow Mathematical Journal,
Vol. 30,
Issue. 2,
p.
129.
Elias, Norma
1988.
Toeplitz operators on weighted Bergman spaces.
Integral Equations and Operator Theory,
Vol. 11,
Issue. 3,
p.
310.
Axler, Sheldon
and
Bourdon, Paul
1988.
Finite-codimensional invariant subspaces of Bergman spaces.
Transactions of the American Mathematical Society,
Vol. 306,
Issue. 2,
p.
805.
Upmeier, Harald
1991.
Mappings of Operator Algebras.
p.
275.
Faour, N. S.
1992.
A class of operators associated with L h 2.
Acta Mathematica Hungarica,
Vol. 60,
Issue. 3-4,
p.
247.
Stroethoff, Karel
and
Zheng, De Chao
1992.
Toeplitz and Hankel operators on Bergman spaces.
Transactions of the American Mathematical Society,
Vol. 329,
Issue. 2,
p.
773.
Engliš, Miroslav
1992.
Density of algebras generated by Toeplitz operators on Bergman spaces.
Arkiv för Matematik,
Vol. 30,
Issue. 1-2,
p.
227.
Klimek, Slawomir
and
Lesniewski, Andrzej
1992.
Quantum Riemann surfaces I. The unit disc.
Communications in Mathematical Physics,
Vol. 146,
Issue. 1,
p.
103.
Aleman, Alexandru
1992.
Invariant subspaces with finite codimension in Bergman spaces.
Transactions of the American Mathematical Society,
Vol. 330,
Issue. 2,
p.
531.
Ross, William T.
1993.
The commutant of a certain compression.
Proceedings of the American Mathematical Society,
Vol. 118,
Issue. 3,
p.
831.
Borthwick, David
Klimek, Slawomir
Lesniewski, Andrzej
and
Rinaldi, Maurizio
1993.
Super Toeplitz operators and non-perturbative deformation quantization of supermanifolds.
Communications in Mathematical Physics,
Vol. 153,
Issue. 1,
p.
49.
Böttcher, Albrecht
1993.
Toeplitz Operators on the Disk with Locally Sectorial Symbols.
Rocky Mountain Journal of Mathematics,
Vol. 23,
Issue. 3,
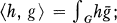 the norm ‖h‖2 of a function h in L2(G) is given by ‖h‖2 = (∫G|h|2)1/2.
the norm ‖h‖2 of a function h in L2(G) is given by ‖h‖2 = (∫G|h|2)1/2.

