Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T12:07:45.139Z Has data issue: false hasContentIssue false
  • English
  • Français

Tilings of Normed Spaces

Published online by Cambridge University Press:  20 November 2018

Carlo Alberto De Bernardi  and
Libor Veselý
Carlo Alberto De Bernardi
Affiliation:
Dipartimento di Matematica, Università degli Studi, Via C. Saldini 50, 20133 Milano e-mail: [email protected], [email protected]
Libor Veselý
Affiliation:
Dipartimento di Matematica, Università degli Studi, Via C. Saldini 50, 20133 Milano e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By a tiling of a topological linear space $X$, we mean a covering of $X$ by at least two closed convex sets, called tiles, whose nonempty interiors are pairwise disjoint. Study of tilings of infinite dimensional spaces was initiated in the 1980's with pioneer papers by V. Klee. We prove some general properties of tilings of locally convex spaces, and then apply these results to study the existence of tilings of normed and Banach spaces by tiles possessing certain smoothness or rotundity properties. For a Banach space $X$, our main results are the following.

  • (i) $X$ admits no tiling by Fréchet smooth bounded tiles.

  • (ii) If $X$ is locally uniformly rotund $\left( \text{LUR} \right)$, it does not admit any tiling by balls.

  • (iii) On the other hand, some 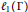${{\ell }_{1}}\left( \Gamma \right)$ spaces, $\Gamma $ uncountable, do admit a tiling by pairwise disjoint $\text{LUR}$ bounded tiles.

Keywords

46B2052A9946A45tiling of normed spaceFréchet smooth bodylocally uniformly rotund bodyl1(Γ)- spaces
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 2 , 01 April 2017 , pp. 321 - 337
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Amir, D. and Deutsch, F., Suns, moons, and quasi-polyhedra. J. Approx. Theory 6(1972), 176–201. http://dx.doi.org/10.1016/0021-9045(72)90073-1 Google Scholar
[2] De Bernardi, C. A. and Vesely, L., On support points and support functionals of convex sets. Israel J. Math. 171(2009), 15–27. http://dx.doi.Org/10.1007/s11856-009-0037-6 Google Scholar
[3] Engelking, R., General topology. Second edition. Sigma Series in Pure Mathematic, 6, Heldermann Verlag, Berlin, 1989.Google Scholar
[4] Fabian, M., Habala, P., Hájek, P., Montesinos, V., and Zizler, V., Banach space theory. The basis for linear and nonlinear analysis, CMS Books in Mathematics/Ouvrages de Mathématiques de la SMC, Springer, New York, 2011.Google Scholar
[5] Fonf, V. P., Three characterizations of polyhedral Banach spaces. (Russian) Ukrain. Mat. Zh. 42 (1990), 1286–1290; translation in Ukrainian Math. J. 42 (1990), 1145-1148 (1991). http://dx.doi.org/=10.1007/BF01056615 Google Scholar
[6] Fonf, V. P., Pezzotta, A., and Zanco, C., Tiling infinite-dimensional normed spaces, Bull. London Math. Soc. 29(1997), 713–719. http://dx.doi.Org/10.1112/S0024609397003196 Google Scholar
[7] Fonf, V. P. and Zanco, C., Covering a Banach space. Proc. Amer. Math. Soc. 134(2006), 2607–2611. http://dx.doi.org/10.1090/S0002-9939-06-08254-2 Google Scholar
[8] Klee, V. L., Dispersed Chebyshev sets and coverings by balls. Math. Ann. 257(1981), 251–260.http://dx.doi.org/10.1007/BF01458288 Google Scholar
[9] Klee, V. L., Do infinite-dimensional Banach spaces admit nice tilings? Studia Sci. Math. Hungar. 21(1986), 415–427.Google Scholar
[10] Klee, V. L., Maluta, E., and Zanco, C., Tiling with smooth and rotund tiles, Fund. Math. 126 (1986), 269–290.Google Scholar
[11] Klee, V. L. and Tricot, C., Locally countable plump tilings are flat. Math. Ann. 277(1987),315–325. http://dx.doi.Org/10.1007/BF01457365 Google Scholar
[12] Marchese, A. and Zanco, C., On a question by Corson about point-finite coverings. Israel J. Math. 189(2012), 55–63. http://dx.doi.Org/10.1007/s11856-011-0126-1 Google Scholar
[13] Preiss, D., Tilings ofHilbert spaces. Mathematika 56(2010), 217–230. http://dx.doi.org/10.1112/S0025579310000562 Google Scholar