Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Herstein, I. N.
1953.
A Theorem on Rings.
Canadian Journal of Mathematics,
Vol. 5,
Issue. ,
p.
238.
Nakayama, Tadasi
1953.
On the Commutativity of Certain Division Rings.
Canadian Journal of Mathematics,
Vol. 5,
Issue. ,
p.
242.
Rosenberg, Alex
and
Zelinsky, Daniel
1954.
On Nakayama’s extension of the 𝑥^{𝑛(𝑥)} theorems.
Proceedings of the American Mathematical Society,
Vol. 5,
Issue. 3,
p.
484.
Herstein, I. N.
1955.
A Theorem Concerning Three Fields.
Canadian Journal of Mathematics,
Vol. 7,
Issue. ,
p.
202.
Von Nakayama, Tadasi
1955.
Über die Kommutativität gewisser Ringe.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 20,
Issue. 1-2,
Drazin, M. P.
1957.
A generalization of polynomial identities in rings.
Proceedings of the American Mathematical Society,
Vol. 8,
Issue. 2,
p.
352.
Drazin, M. P.
1957.
Rings with nil commutator ideals.
Rendiconti del Circolo Matematico di Palermo,
Vol. 6,
Issue. 1,
p.
51.
Drazin, M. P.
1958.
Rings with Central Idempotent or Nilpotent Elements.
Proceedings of the Edinburgh Mathematical Society,
Vol. 9,
Issue. 4,
p.
157.
Faith, Carl
1960.
Algebraic division ring extensions.
Proceedings of the American Mathematical Society,
Vol. 11,
Issue. 1,
p.
43.
Schenkman, Eugene
and
Scott, W. R.
1960.
A generalization of the Cartan-Brauer-Hua theorem.
Proceedings of the American Mathematical Society,
Vol. 11,
Issue. 3,
p.
396.
Faith, Carl
1961.
Radical extensions of rings.
Proceedings of the American Mathematical Society,
Vol. 12,
Issue. 2,
p.
274.
Inatomi, Akira
1962.
On generating elements of simple algebras.
Kodai Mathematical Journal,
Vol. 14,
Issue. 3,
Slater, M
1964.
On simple rings satisfying a type of “restricted” polynomial identity.
Journal of Algebra,
Vol. 1,
Issue. 4,
p.
347.
Asano, Shigemoto
1966.
On invariant subspaces of division algebras.
Kodai Mathematical Journal,
Vol. 18,
Issue. 4,
Ellers, Erich
1969.
Eine Bemerkung über zweiseitige Inzidenzgruppen.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 33,
Issue. 1-2,
p.
1.
Rogers, Kenneth
1971.
An elementary proof of a theorem of Jacobson.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 35,
Issue. 3-4,
p.
223.
Loustau, J.A
1974.
Radical extensions of Jordan rings.
Journal of Algebra,
Vol. 30,
Issue. 1-3,
p.
1.
Chacron, M.
Lawrence, J.
and
Madison, D.
1975.
A Note on Radical Extensions of Rings.
Canadian Mathematical Bulletin,
Vol. 18,
Issue. 3,
p.
423.
Herstein, I. N.
1975.
On a Result of Faith.
Canadian Mathematical Bulletin,
Vol. 18,
Issue. 4,
p.
609.
Herstein, I.N
1975.
On the hypercenter of a ring.
Journal of Algebra,
Vol. 36,
Issue. 1,
p.
151.


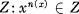 . Then A is commutative.
. Then A is commutative.