Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T13:21:53.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Ternary Diophantine Equations via Galois Representations and Modular Forms

Published online by Cambridge University Press:  20 November 2018

Michael A. Bennett  and
Chris M. Skinner
Michael A. Bennett
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC, V6T 1Z2
Chris M. Skinner
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

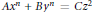In this paper, we develop techniques for solving ternary Diophantine equations of the shape $A{{x}^{n}}+B{{y}^{n}}=C{{z}^{2}}$, based upon the theory of Galois representations and modular forms. We subsequently utilize these methods to completely solve such equations for various choices of the parameters 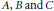$A,\,B\,\text{and}\,\text{C}$. We conclude with an application of our results to certain classical polynomial-exponential equations, such as those of Ramanujan–Nagell type.

Keywords

11D4111F1111G05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 1 , 01 February 2004 , pp. 23 - 54
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Bauer, M. and Bennett, M. A., Applications of the hypergeometric method to the generalized Ramanujan–Nagell equation. Ramanujan J. 6(2002), 209–270.Google Scholar
[2] Beukers, F., On the generalized Ramanujan–Nagell equation I. Acta Arith. 38(1980/1), 389–410.Google Scholar
[3] Bilu, Y., Hanrot, G. and Voutier, P., Existence of primitive divisors of Lucas and Lehmer numbers. J. Reine Angew.Math. 539(2001), 75–122.Google Scholar
[4] Breuil, C., Conrad, B., Diamond, F. and Taylor, R., On the modularity of elliptic curves over Q : wild 3-adic exercises. J. Amer. Math. Soc. 14(2001), 843–939.Google Scholar
[5] Bruin, N., Chabauty methods and covering techniques applied to the generalised Fermat equation. Ph.D. Thesis, Leiden Univ. Leiden, Netherlands, 1999.Google Scholar
[6] Bruin, N., Some low degree ternary equations of signature (p; p; 2). Preprint.Google Scholar
[7] Bugeaud, Y., On some exponential Diophantine equations. Monatsh. Math. 132(2001), 193–197.Google Scholar
[8] Bugeaud, Y. and Shorey, T., On the number of solutions of the generalized Ramanujan–Nagell equation. J. Reine Angew. Math. 539(2001), 55–74.Google Scholar
[9] Cao, Z., On the Diophantine equation x 2 n – Dy2 = 1. Proc. Amer. Math. Soc. (1) 98(1986), 11–16.Google Scholar
[10] Coghlan, F., Elliptic curves with conductor N = 2a3b. Ph.D. Thesis, Univ. Manchester, Manchester, 1967.Google Scholar
[11] Cohn, J. H. E., The Diophantine equation x 2 + C = yn. Acta Arith. 65(1993), 367–381 Google Scholar
[12] Conrad, B., Diamond, F. and Taylor, R., Modularity of certain potentially Barsotti–Tate Galois representations. J. Amer. Math. Soc. 12(1999), 521–567.Google Scholar
[13] Cremona, J., Algorithms for Modular Elliptic Curves. Cambridge University Press, 1992.Google Scholar
[14] Darmon, H., On the equations xn + yn = z2 and xn + yn = z3 . Internat. Math. Res. Notices 72(1993), 263–274.Google Scholar
[15] Darmon, H., The equation x4 – y4 = zp . C. R. Math. Rep. Acad. Sci. Canada 15(1993), 286–290.Google Scholar
[16] Darmon, H., Modularity of fibres in rigid local systems. Ann. of Math. 149(1999), 1079–1086.Google Scholar
[17] Darmon, H., Rigid local systems, Hilbert modular forms, and Fermat's Last Theorem. Duke Math. J. 102(2000), 413–449.Google Scholar
[18] Darmon, H. and Granville, A., On the equations xp + yq = zr and zm = f (x, y). Bull. London Math. Soc. 27(1995), 513–544.Google Scholar
[19] Darmon, H. and Merel, L., Winding quotients and some variants of Fermat's Last Theorem. J. Reine Angew.Math. 490(1997), 81–100.Google Scholar
[20] Diamond, F., On deformation rings and Hecke rings. Ann. of Math. 144(1996), 137–166.Google Scholar
[21] Diamond, F., The refined conjecture of Serre. In: Elliptic Curves, Modular Forms, and Fermat's Last Theorem (ed. Coates, J.), International Press, Cambridge, MA, 1995, 22–37.Google Scholar
[22] Ellenberg, J., Galois representations attached to Q-curves and the generalized Fermat equation A 4 + B 2 = Cp . Amer. J. Math., to appear.Google Scholar
[23] Frey, G., Links between stable elliptic curves and certain Diophantine equations. Ann. Univ. Sarav. Ser. Math. (1) 1, 1986.Google Scholar
[24] Halberstadt, E. and Kraus, A., Courbes de Fermat: résultats et problèmes. J. Reine Angew.Math. 548(2002), 167–234.Google Scholar
[25] Hellegouarch, Y., Sur l'équation diophantienne . C. R. Acad. Sci. Paris Sér. A–B 274(1972), A1385–A1387.Google Scholar
[26] Ivorra, W., Sur les équations xp + 2β yp = z 2 et xp + 2β yp = 2z 2 . Preprint.Google Scholar
[27] Ivorra, W., Personal communication.Google Scholar
[28] Ko, Chao, On the Diophantine equation x 2 = yn + 1, xy ≠ 0. Sci. Sinica 14(1965), 457–460.Google Scholar
[29] Kraus, A., Sur les équations ap + bp + 15cp = 0 et ap + 3bp + 5cp = 0. C. R. Acad. Sci. Paris Sér. I Math. (9) 322(1996), 809–812.Google Scholar
[30] Kraus, A., Sur l'équation a 3 + b 3 = cp . Experiment. Math. (1) 7(1998), 1–13.Google Scholar
[31] Kraus, A., Majorations effectives pour l'équation de Fermat généralisée. Canad. J. Math (6) 49(1997), 1139–1161.Google Scholar
[32] Kraus, A., On the equation xp + yq = zr : a survey. Ramanujan J. (3) 3(1999), 315–333.Google Scholar
[33] Kubert, D., Universal bounds on torsion of elliptic curves. Proc. London Math. Soc. (3) 33(1976), 193–237.Google Scholar
[34] Le, Maohua, On the number of solutions of the generalized Ramanujan–Nagell equation x2 – D = 2n+2 . Acta Arith. 60(1991), 149–167.Google Scholar
[35] Le, Maohua, On the generalized Ramanujan–Nagell equation x2 – D = 2n+2 . Trans. Amer. Math. Soc. 334(1992), 809–825.Google Scholar
[36] Le, Maohua, The Diophantine equation x2 + Dm = 2n+2 . Comment. Math. Univ. St. Paul. 43(1994), 127–133.Google Scholar
[37] Lesage, J.-L., Différence entre puissances et carrés d'entiers. J. Number Theory (2) 73(1998), 390–425.Google Scholar
[38] Ljunggren, W., On the Diophantine equation Cx2 + D = yn . Pacific J. Math. 14(1964), 585–596.Google Scholar
[39] Mazur, B., Rational isogenies of prime degree. Invent. Math. 44(1978), 129–162.Google Scholar
[40] Merel, L., Arithmetic of elliptic curves and Diophantine equations. J. Théor. Nombres Bordeaux 11(1999), 173–200.Google Scholar
[41] Mignotte, M. and deWeger, B. M. M., On the Diophantine equations x2 + 74 = y5 and x2 + 86 = y5 . Glasgow Math. J. (1) 38(1996), 77–85.Google Scholar
[42] Miyake, T., Modular Forms. Springer-Verlag, Berlin-New York, 1988.Google Scholar
[43] Momose, F., Rational points on the modular curves X Split(p) . Compositio Math. 52(1984), 115–137.Google Scholar
[44] Mordell, L. J., Diophantine Equations. Academic Press, London, 1969.Google Scholar
[45] Nagell, T., The diophantine equation x2 + 7 = 2n . Ark. Math. 4(1960), 185–187.Google Scholar
[46] Papadopolous, I., Sur la classification de Neron des courbes elliptiques en caracteristique residuelle 2 et 3. J. Number Theory 44(1993), 119–152.Google Scholar
[47] Poonen, B., Some Diophantine equations of the form xn + yn = zm . Acta Arith. 86(1998), 193–205.Google Scholar
[48] Ramanujan, S., Question 464. J. Indian Math. Soc. 5(1913), 120.Google Scholar
[49] Ribet, K., On the equation ap + 2αbp + cp = 0. Acta Arith. 79(1997), 7–16.Google Scholar
[50] Rodeja, F. E. G., On the diophantine equation x3 + y3 = 2z 2 . (Spanish) Revista Mat. Hisp.-Amer. (4) 13(1953), 229–240.Google Scholar
[51] Serre, J.-P., Sur les représentations modulaires de degré 2 de . Duke Math. J. 54(1987), 179–230.Google Scholar
[52] Silverman, J., The Arithmetic of Elliptic Curves. Graduate Texts in Math. 106, Springer-Verlag, Berlin-New York, 1986.Google Scholar
[53] Silverman, J., Advanced Topics in the Arithmetic of Elliptic Curves. Graduate Texts in Math. 151, Springer-Verlag, Berlin-New York, 1994.Google Scholar
[54] Stein, W., Modular forms database. Current web address http://modular.fas.harvard.edu/Tables/ Google Scholar
[55] Wiles, A., Modular elliptic curves and Fermat's last theorem. Ann. of Math. (2) 141(1995), 443–551.Google Scholar