Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T07:47:14.110Z Has data issue: false hasContentIssue false
  • English
  • Français

Term by Term Dyadic Differentiation

Published online by Cambridge University Press:  20 November 2018

Charles H. Powell  and
William R. Wade
Charles H. Powell
Affiliation:
The University of Tennessee, Knoxville, Tennessee
William R. Wade
Affiliation:
The University of Tennessee, Knoxville, Tennessee
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ψ0, ψ1, … denote the Walsh-Paley functions and let ∔ denote the group operation which Fine [5] defined on the interval [0, 1). Thus, if k ≧ 0 is an integer and if u, t are points in the interval [0, 1) then

(where αk = 0 or 1 represents the kth coefficient of the binary expansion of t), and

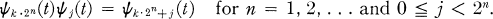
A real-valued function ƒ, is said to be dyadically differentiable at a point x ∈ [0, 1) if ƒ is defined at x and at x ∔ 2–n–1, n = 0, 1, …;, and if the sequence

(1)

converges as N → ∞.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 1 , 01 February 1981 , pp. 247 - 256
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Butzer, P. L. and Wagner, H. J., Walsh-Fourier series and the concept of a derivative, Applicable Anal. 3 (1973), 29–46.Google Scholar
2. Butzer, P. L. and Wagner, H. J., On dyadic analysis based on the pointwise dyadic derivative, Analysis Math. 1 (1975), 171–196.Google Scholar
3. Coury, J. E., Walsh series with coefficients tending monotonically to zero, Pacific J. Math. 54 (1974), 1–16.Google Scholar
4. Coury, J. E., On the Walsh-Fourier coefficients of certain classes of functions, to appear.Google Scholar
5. Fine, N. J., On the Walsh Functions, Trans. Amer. Math. Soc. 65 (1949), 372–414.Google Scholar
6. Morgenthaler, G. W., On Walsh-Fourier series, Trans. Amer. Math. Soc. 84 (1957), 472–507.Google Scholar
7. Schipp, F., On term by term dyadic differentiation of Walsh series, Analysis Math. 2 (1976), 149–154.Google Scholar
8. Sölin, P., An inequality of Paley and convergence a.e. of Walsh-Fourier series, Ark. fur Mat. 7 (1969), 551–570.Google Scholar
9. Steckin, S. and Ul'janov, P. L., On sets of uniqueness, Izv. Akad. Nauk SSSR, Ser. Mat. 26 (1962), 211–222.Google Scholar