Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T00:48:34.312Z Has data issue: false hasContentIssue false
  • English
  • Français

A Technique to Generate 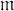-Ary Free Lattices from Finitary Ones

Published online by Cambridge University Press:  20 November 2018

George Grätzer  and
David Kelly
George Grätzer
Affiliation:
University of Manitoba, Winnipeg, Manitoba
David Kelly
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 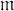be an infinite regular cardinal. A poset L is called an 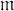-lattice if and only if for all XL satisfying 0 < |X| < m, ∧ X and ∨ X exist.

This paper is a part of a sequence of papers, [5], [6], [7], [8], developing the theory of 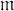-lattices. For a survey of some of these results, see [9].

The 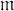-lattice is described in [6]; γ denotes the zero and γ′ the unit of . In particular, formulas for 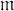-joins and meets are given. (We repeat the essentials of this description in Section 4.)

In [6] we proved the theorem stated below. Our proof was based on characterization of 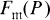(the free 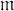-lattice on P) due to [1]; as a result, our proof was very computational.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 2 , 01 April 1985 , pp. 324 - 336
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Crawley, P. and Dean, R. A., Free lattices with infinite operations. Trans. Amer. Math. Soc. 92 (1959), 35–47.Google Scholar
2. Funayama, N., Notes on lattice theory IV. On partial (semi-) lattices, Bull. Yamagata Univ. (Nat. Sei.) 2 (1953), 171–184.Google Scholar
3. Grätzer, G., Universal algebra, Second Edition (Springer Verlag, New York, Heidelberg, Berlin, 1979).Google Scholar
4. Grätzer, G., General lattice theory. Pure and Applied Mathematics Series, Academic Press, New York, N.Y.; Mathematische Reihe, Band 52, Birkhauser Verlag, Basel; Akademie Verlag, Berlin, 1978. (Russian translation: MIR Publishers, Moscow, 1982.)Google Scholar
5. Grätzer, G. and Kelly, D., Free m-products of lattices. I and II, Colloq. Math., to appear.Google Scholar
6. Grätzer, G. and Kelly, D., The free m-lattice on the poset H, ORDER I (1984), 47–65.Google Scholar
7. Grätzer, G. and Kelly, D., An embedding theorem for free m-lattices on slender posets. Google Scholar
8. Grätzer, G. and Kelly, D., A description of free m-lattices on slender posets. Google Scholar
9. Grätzer, G. and Kelly, D., The construction of some free m-lattices on posets, Orders: Descriptions and Roles (Proceedings of the 1982 conference on ordered sets and their applications), (North-Holland, Amsterdam, 1984), 103–118.Google Scholar
10. Rival, I. and Willer, R., Lattices freely generated by partially ordered sets: which can be “drawn“?, J. Reine. Angew. Math. 310 (1979), 56–80.Google Scholar