Let $\Xi $ be a discrete set in 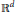${{\mathbb{R}}^{d}}$. Call the elements of $\Xi $centers. The well-known Voronoi tessellation partitions 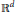${{\mathbb{R}}^{d}}$ into polyhedral regions (of varying volumes) by allocating each site of 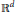${{\mathbb{R}}^{d}}$ to the closest center. Here we study allocations of 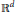${{\mathbb{R}}^{d}}$ to $\Xi $ in which each center attempts to claim a region of equal volume $\alpha $.

We focus on the case where $\Xi $ arises from a Poisson process of unit intensity. In an earlier paper by the authors it was proved that there is a unique allocation which is stable in the sense of the Gale–Shapley marriage problem. We study the distance 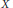$X$ from a typical site to its allocated center in the stable allocation.

The model exhibits a phase transition in the appetite $\alpha $. In the critical case 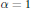$\alpha \,=\,1$ we prove a power law upper bound on 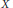$X$ in dimension 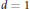$d\,=\,1$. (Power law lower bounds were proved earlier for all 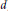$d$). In the non-critical cases 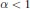$\alpha <1$ and 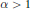$\alpha \,>1$we prove exponential upper bounds on 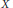$X$.