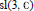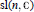Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
MAZORCHUK, VOLODYMYR
2003.
QUANTUM DEFORMATION AND TABLEAUX REALIZATION OF SIMPLE DENSE ${\mathfrak g} l (n, {\mathbb C})$-MODULES.
Journal of Algebra and Its Applications,
Vol. 02,
Issue. 01,
p.
1.
Mazorchuk, Volodymyr
and
Stroppel, Catharina
2011.
Cuspidalsln-modules and deformations of certain Brauer tree algebras.
Advances in Mathematics,
Vol. 228,
Issue. 2,
p.
1008.
Futorny, Vyacheslav
Grantcharov, Dimitar
and
Ramirez, Luis Enrique
2016.
Singular Gelfand–Tsetlin modules of gl(n).
Advances in Mathematics,
Vol. 290,
Issue. ,
p.
453.
Futorny, Vyacheslav
Grantcharov, Dimitar
and
Ramirez, Luis Enrique
2017.
New Singular Gelfand–Tsetlin $${\mathfrak{gl}(n)}$$ gl ( n ) -Modules of Index 2.
Communications in Mathematical Physics,
Vol. 355,
Issue. 3,
p.
1209.
Futorny, Vyacheslav
Ramirez, Luis Enrique
and
Zhang, Jian
2018.
Gelfand–Tsetlin modules of quantum gln defined by admissible sets of relations.
Journal of Algebra,
Vol. 499,
Issue. ,
p.
375.
Futorny, Vyacheslav
Ramirez, Luis Enrique
and
Zhang, Jian
2019.
Combinatorial construction of Gelfand–Tsetlin modules for gln.
Advances in Mathematics,
Vol. 343,
Issue. ,
p.
681.
Futorny, Vyacheslav
Ramirez, Luis Enrique
and
Zhang, Jian
2019.
Explicit construction of irreducible modules for
$$U_q(\mathfrak {gl}_n)$$
U
q
(
gl
n
)
.
São Paulo Journal of Mathematical Sciences,
Vol. 13,
Issue. 1,
p.
83.
Futorny, Vyacheslav
Grantcharov, Dimitar
and
Ramirez, Luis Enrique
2019.
Drinfeld category and the classification of singular Gelfand–Tsetlin $\displaystyle \mathfrak{gl}_n$-modules.
International Mathematics Research Notices,
Vol. 2019,
Issue. 5,
p.
1463.
Early, Nick
Mazorchuk, Volodymyr
and
Vishnyakova, Elizaveta
2020.
Canonical Gelfand–Zeitlin Modules over Orthogonal Gelfand–Zeitlin Algebras.
International Mathematics Research Notices,
Vol. 2020,
Issue. 20,
p.
6947.
Futorny, Vyacheslav
Grantcharov, Dimitar
Ramirez, Luis Enrique
and
Zadunaisky, Pablo
2020.
Gelfand-Tsetlin theory for rational Galois algebras.
Israel Journal of Mathematics,
Vol. 239,
Issue. 1,
p.
99.
Futorny, Vyacheslav
Grantcharov, Dimitar
and
Ramirez, Luis Enrique
2021.
Classification of simple Gelfand–Tsetlin modules of 𝔰𝔩(3).
Bulletin of Mathematical Sciences,
Vol. 11,
Issue. 03,
Futorny, Vyacheslav
Hernández Morales, Oscar Armando
and
Ramirez, Luis Enrique
2022.
Simple Modules for Affine Vertex Algebras in the Minimal Nilpotent Orbit.
International Mathematics Research Notices,
Vol. 2022,
Issue. 20,
p.
15788.
Futorny, Vyacheslav
2022.
Representations of Lie algebras.
São Paulo Journal of Mathematical Sciences,
Vol. 16,
Issue. 1,
p.
131.