Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
van Zanten, A. J.
and
de Vries, E.
1974.
On The Number of Classes of a Finite Group Invariant for Certain Substitutions.
Canadian Journal of Mathematics,
Vol. 26,
Issue. 5,
p.
1090.
Stedman, G E
1975.
A diagram technique for coupling calculations in compact groups.
Journal of Physics A: Mathematical and General,
Vol. 8,
Issue. 7,
p.
1021.
Butler, P. H.
and
Wybourne, B. G.
1976.
Calculation of j and jm symbols for arbitrary compact groups. I. Methodology.
International Journal of Quantum Chemistry,
Vol. 10,
Issue. 4,
p.
581.
Kibler, M. R.
and
Guichon, P. A. M.
1976.
Clebsch‐Gordan coefficients for chains of groups of interest in quantum chemistry.
International Journal of Quantum Chemistry,
Vol. 10,
Issue. 1,
p.
87.
Butler, P. H.
and
Wybourne, B. G.
1976.
Calculation of j and jm symbols for arbitrary compact groups. III. Application to SO3 ⊃ T ⊃ C3 ⊃ C1.
International Journal of Quantum Chemistry,
Vol. 10,
Issue. 4,
p.
615.
Backhouse, Nigel
1977.
Computers in Nonassociative Rings and Algebras.
p.
279.
Bickerstaff, R P
and
Wybourne, B G
1978.
Commuting tensor operators and the state labelling problem for SO(4)⊃P.
Journal of Physics A: Mathematical and General,
Vol. 11,
Issue. 2,
p.
231.
Prasad, L S R K
and
Bharathi, K
1979.
6j, 9j symbols and 3jm factors for the group chainD 5 ⊃C 5.
Pramana,
Vol. 13,
Issue. 6,
p.
653.
Vaughn, M T
1979.
Massless fermion representations in grand unified gauge theories.
Journal of Physics G: Nuclear Physics,
Vol. 5,
Issue. 10,
p.
1317.
Butler, Philip H.
1979.
Recent Advances in Group Theory and Their Application to Spectroscopy.
p.
123.
Prasad, L S R K
and
Bharathi, K
1980.
6j symbols and 3jm factors for the group chain D4dcontains/implies D4contains/implies C4.
Journal of Physics A: Mathematical and General,
Vol. 13,
Issue. 3,
p.
781.
Butler, Philip H.
1980.
Symmetries in Science.
p.
89.
Newmarch, J. D.
and
Golding, R. M.
1981.
The Racah algebra for groups with time reversal symmetry .II.
Journal of Mathematical Physics,
Vol. 22,
Issue. 10,
p.
2113.
Bickerstaff, R P
and
Wybourne, B G
1981.
Dissociation calculations for S-wave multiquark systems.
Journal of Physics G: Nuclear Physics,
Vol. 7,
Issue. 3,
p.
275.
Damhus, Ture
1981.
On the existence of real Clebsch–Gordan coefficients.
Journal of Mathematical Physics,
Vol. 22,
Issue. 1,
p.
7.
Bickerstaff, R P
Butler, P H
Butts, M B
Haase, R W
and
Reid, M F
1982.
3jm and 6j tables for some bases of SU6and SU3.
Journal of Physics A: Mathematical and General,
Vol. 15,
Issue. 4,
p.
1087.
Chatterjee, R.
and
Lulek, T.
1982.
Permutational properties of the generalized Clebsch–Gordan coefficients.
Journal of Mathematical Physics,
Vol. 23,
Issue. 6,
p.
922.
Newmarch, J. D.
1983.
On the 3j symmetries.
Journal of Mathematical Physics,
Vol. 24,
Issue. 4,
p.
757.
Mucha, M.
and
Lulek, T.
1983.
Permutational symmetry of Clebsch-Gordan coefficients for the metacyclic groups.
Linear Algebra and its Applications,
Vol. 51,
Issue. ,
p.
49.
Newmarch, J. D.
1983.
Some character theory for groups of linear and antilinear operators.
Journal of Mathematical Physics,
Vol. 24,
Issue. 4,
p.
742.


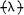 of group
of group