Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T00:36:15.753Z Has data issue: false hasContentIssue false
  • English
  • Français

A Symmetric Proof of the Riemann-Roch Theorem, and a New Form of the Unit Theorem

Published online by Cambridge University Press:  20 November 2018

S. Beatty  and
N. D. Lane
S. Beatty
Affiliation:
University of Toronto, Carleton College
N. D. Lane
Affiliation:
University of Toronto, Carleton College
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let F(z, u) denote

1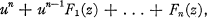

where F1(z),… , Fn(z) are rational functions of z with complex coefficients. We shall speak of F (z, u) = 0 as the fundamental algebraic equation and shall adopt z as the independent variable and u as the dependent, except in § 4, where we use x and y instead of them, and where it is understood that x and y are connected birationally with z and u.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 4 , 1952 , pp. 136 - 148
Copyright
Copyright © Canadian Mathematical Society 1952

References

1. Beatty, S., Derivation of the Complementary Theorem from the Riemann-Roch Theorem, Amer. J. Math., vol. 39 (1917), 257–262.Google Scholar
2. Beatty, S., The algebraic theory of algebraic functions of one variable, Proc. London Math. Soc. (2), vol. 20 (1920), 435–449.Google Scholar
3. Beatty, S., Integral bases for an algebraic function field, J. London Math. Soc, vol. 4 (1928), 13–17.Google Scholar
4. Beatty, S. and Fisher, Miss M. J., Theory of algebraic functions based on a study of fundamental exponents, Scripta Math., vol. 5 (1938), 187-194, 239–245.Google Scholar
5. Chevalley, C., Introduction to the theory of algebraic functions of one variable, Math. Surveys, vol. 6 (1951); in particular, 28–33.Google Scholar
6. Dedekind, R. and Weber, H., Theorie der algebraischen Funktionen einer Veranderlichen, J. Reine Angew. Math., vol. 92 (1882), 181–290.Google Scholar
7. Fields, J. C., Theory of the algebraic functions of a complex variable (Berlin, 1906).Google Scholar
8. Hensel, K. and Landsberg, G., Theorie der algebraischen Funktionen eintr Variabeln (Leipzig, 1902).Google Scholar