Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T13:39:21.287Z Has data issue: false hasContentIssue false
  • English
  • Français

Symbolic Powers Versus Regular Powers of Ideals of General Points in ℙ1 × ℙ1

Published online by Cambridge University Press:  20 November 2018

Elena Guardo ,
Brian Harbourne  and
Adam Van Tuyl
Elena Guardo
Affiliation:
Dipartimento di Matematica e Informatica, Viale A. Doria, 6 - 95100 - Catania, Italy, e-mail: [email protected]
Brian Harbourne
Affiliation:
Department of Mathematics, University of Nebraska–Lincoln, Lincoln, NE 68588-0130, USA, e-mail: [email protected]
Adam Van Tuyl
Affiliation:
Department of Mathematical Sciences, Lakehead University, Thunder Bay, ON P7B 5E1, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recent work of Ein–Lazarsfeld–Smith and Hochster–Huneke raised the problem of which symbolic powers of an ideal are contained in a given ordinary power of the ideal. Bocci–Harbourne developed methods to address this problem, which involve asymptotic numerical characters of symbolic powers of the ideals. Most of the work done up to now has been done for ideals defining 0-dimensional subschemes of projective space. Here we focus on certain subschemes given by a union of lines in ${{\mathbb{P}}^{3}}$ that can also be viewed as points in 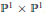${{\mathbb{P}}^{1}}\times {{\mathbb{P}}^{1}}$. We also obtain results on the closely related problem, studied by Hochster and by Li and Swanson, of determining situations for which each symbolic power of an ideal is an ordinary power.

Keywords

13F2013A1514C20symbolic powersmultigradedpoints
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 4 , 01 August 2013 , pp. 823 - 842
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Bocci, C. and Harbourne, B., Comparing powers and symbolic power of ideals. J. Algebraic Geom. 19(2010), no. 3, 399–417. http://dx.doi.org/10.1090/S1056-3911-09-00530-X Google Scholar
[2] Bocci, C., The resurgence of ideals of points and the containment problem. Proc. Amer. Math. Soc. 138(2010), no. 4, 1175–1190. http://dx.doi.org/10.1090/S0002-9939-09-10108-9 Google Scholar
[3] Bocci, C., Cooper, S., and Harbourne, B., Containment results for ideals of various configurations of points in ℙN. arxiv:1109.1884v1. Google Scholar
[4] Chudnovsky, G. V., Singular points on complex hypersurfaces and multidimensional Schwarz lemma. In: Seminar on Number Theory, Paris 1979–80, Progr. Math., 12, Birkhäuser, Boston, MA, 1981, pp. 29–69.Google Scholar
[5] CoCoATeam, CoCoA: a system for doing computations in Commutative Algebra. http://cocoa.dima.unige.it. Google Scholar
[6] Bruns, W., Ichim, B., and Säger, C., Normaliz. Algorithms for rational cones and affine monoids. http://www.math.uos.de/normaliz. Google Scholar
[7] Ein, L., Lazarsfeld, R., and Smith, K. E., Uniform bounds and symbolic powers on smooth varieties. Invent. Math. 144(2001), no. 2, 241–252. http://dx.doi.org/10.1007/s002220100121 Google Scholar
[8] Esnault, H. and Viehweg, E., Sur une minoration du degrá d’hypersurfaces s’annulant en certains points. Math. Ann. 263(1983), no. 1, 75–86.http://dx.doi.org/10.1007/BF01457085 Google Scholar
[9] Fitchett, S., Maps of linear systems on blow-ups of the projective plane. J. Pure Appl. Algebra 156(2001), no. 1, 1–14. http://dx.doi.org/10.1016/S0022-4049(99)00115-2 Google Scholar
[10] Geramita, A., Harbourne, B., and Migliore, J., Classifying Hilbert functions of fat point subschemes in ℙ2. Collect. Math. 60(2009), no. 2, 159–192. http://dx.doi.org/10.1007/BF03191208 Google Scholar
[11] Gimigliano, A., Harbourne, B., and Idà, M., Betti numbers for fat point ideals in the plane: a geometric approach. Trans. Amer. Math. Soc. 361(2009), no. 2, 1103–1127.http://dx.doi.org/10.1090/S0002-9947-08-04599-6 Google Scholar
[12] Giuffrida, S., Maggioni, R., and Ragusa, A., On the postulation of 0-dimensional subschemes on a smooth quadric. Pacific J. Math. 155(1992), no. 2, 251–282.Google Scholar
[13] Grayson, D. R. and Stillman, M. E., Macaulay 2, a software system for research in algebraic geometry. http://www.math.uiuc.edu/Macaulay2/. Google Scholar
[14] Guardo, E., Fat point schemes on a smooth quadric. J. Pure Appl. Algebra 162(2001), no. 2–3, 183–208. http://dx.doi.org/10.1016/S0022-4049(00)00123-7 Google Scholar
[15] Guardo, E. and Harbourne, B., Resolutions of ideals of six fat points in ℙ2. J. Algebra 318(2007), no. 2, 619–640. http://dx.doi.org/10.1016/j.jalgebra.2007.09.018 Google Scholar
[16] Guardo, E., Harbourne, B., and Van Tuyl, A., Asymptotic resurgences for ideals of positive dimensional subschemes of projective space. arxiv:1202.4370v1. Google Scholar
[17] Guardo, E., Fat lines in ℙ3: powers versus symbolic powers. arxiv:1208.5221v1. Google Scholar
[18] Guardo, E. and Van Tuyl, A., Fat points in ℙ1 ✗ ℙ1 and their Hilbert functions. Canad. J. Math. 56(2004), no. 4, 716–741. http://dx.doi.org/10.4153/CJM-2004-033-0 Google Scholar
[19] Harbourne, B., Birational models of rational surfaces. J. Algebra 190(1997), 145–162. http://dx.doi.org/10.1006/jabr.1996.6899 Google Scholar
[20] Harbourne, B., Free Resolutions of Fat Point Ideals on P2. J. Pure Appl. Algebra 125(1998), no. 1–3, 213–234. http://dx.doi.org/10.1016/S0022-4049(96)00126-0 Google Scholar
[21] Harbourne, B. and Huneke, C., Are symbolic powers highly evolved? J. Ramanujan Math. Soc., to appear. arxiv:1103.5809v1. Google Scholar
[22] Hochster, M., Criteria for the equality of ordinary and symbolic powers of primes. Math. Z. 133(1973), 53–65.http://dx.doi.org/10.1007/BF01226242 Google Scholar
[23] Hochster, M. and Huneke, C., Comparison of symbolic and ordinary powers of ideals. Invent. Math. 147(2002), no. 2, 349–369. http://dx.doi.org/10.1007/s002220100176 Google Scholar
[24] Li, A. and Swanson, I., Symbolic powers of radical ideals. Rocky Mountain J. Math. 36(2006), no. 3, 997–1009. http://dx.doi.org/10.1216/rmjm/1181069441 Google Scholar
[25] Marino, L., Conductor and separating degrees for sets of points in ℙr and in ℙ1 ✗ ℙ1. Boll. Unione Mat. Ital. Sez. B Artic. Ric. Mat. (8) 9(2006), no. 2, 397–421.Google Scholar
[26] Mumford, D., Varieties defined by quadratic equations. In: Questions on algebraic varieties (C.I.M.E., III Ciclo, Varenna, 1969) Edizioni Cremonese, Rome, 1970, pp. 30–100.Google Scholar
[27] Schwede, K., A canonical linear system associated to adjoint divisors in characteristic p>0. arxiv:1107.3833v1. 0.+arxiv:1107.3833v1.>Google Scholar
[28] Sidman, J. and Van Tuyl, A., Multigraded regularity: syzygies and fat points. Beiträge Algebra Geom. 47(2006), no. 1, 67–87.Google Scholar
[29] Skoda, H., Estimations L2 pour l'opérateur et applications arithmétiques. In: Journée sur les Fonctions Analytiques (Toulouse, 1976), Lecture Notes in Math., 578, Springer, Berlin, 1977, pp. 314–323.Google Scholar
[30] Van Tuyl, A., The defining ideal of a set of points in multi-projective space. J. London Math. Soc. (2) 72(2005), no. 1, 73–90.http://dx.doi.org/10.1112/S0024610705006459 Google Scholar
[31] Van Tuyl, A., An appendix to a paper of Catalisano, Geramita, Gimigliano: The Hilbert function of generic sets of 2-fat points in ℙ1 ✗ ℙ1. In: Projective Varieties with Unexpected Properties. de Gruyter, Berlin, 2005, pp. 109–112.Google Scholar
[32] Waldschmidt, M., Propriétés arithmétiques de fonctions de plusieurs variables. II. In: Séminaire Pierre Lelong (Analyse), 1975–76, Lecture Notes Math. 578, Springer, Berlin, 1977, pp. 108–135.Google Scholar
[33] Waldschmidt, M., Nombres transcendants et groupes algébriques, Astérisque 69/70, Sociéte Mathématiqué de France, Paris, 1979.Google Scholar
[34] Zariski, O. and Samuel, P., Commutative algebra. Vol. II. The University Series in Higher Mathematics, D. Van Nostrand Co., Inc., Princeton, NJ-Toronto-London-New York, 1960.Google Scholar