Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T00:44:14.420Z Has data issue: false hasContentIssue false
  • English
  • Français

Suspension of the Lusternik-Schnirelmann Category

Published online by Cambridge University Press:  20 November 2018

William J. Gilbert
William J. Gilbert*
Affiliation:
University of Waterloo, Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let cat be the Lusternik-Schnirelmann category structure as defined by Whitehead [6] and let be the category structure as defined by Ganea [2],

We prove that

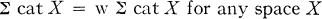
and

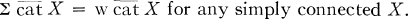
It is known that w ∑ cat X = conil X for connected X. Dually, if X is simply connected,

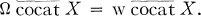
1. We work in the category of based topological spaces with the based homotopy type of CW-complexes and based homotopy classes of maps. We do not distinguish between a map and its homotopy class. Constant maps are denoted by 0 and identity maps by 1.

We recall some notions from Peterson's theory of structures [5; 1] which unify the definitions of the numerical homotopy invariants akin to the Lusternik-Schnirelmann category.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 6 , 01 December 1970 , pp. 1129 - 1132
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Berstein, I. and Hilton, P. J., Homomorphisms of homotopy structures, Topologie et géométrie différentielle, Séminaire C. Ehresmann, Vol. 5 (Institut H. Poincaré, Paris, 1963).Google Scholar
2. Ganea, T., A generalization of the homology and homotopy suspension, Comment. Math. Helv. 39 (1965), 295–322.Google Scholar
3. Ganea, T., Hilton, P. J., and Peterson, F. P., On the homotopy-commutativity of loop spaces and suspensions, Topology 1 (1962), 133–141.Google Scholar
4. Gilbert, W. J., Some examples for weak category and conilpotency, Illinois J. Math. 12 (1968), 421–432.Google Scholar
5. Peterson, F. P., Numerical invariants of homotopy type, pp. 79–83 in Colloquium on Algebraic Topology (Matematisk Institut, Aarhus Univ., Aarhus, 1962).Google Scholar
6. Whitehead, G. W., The homology suspension, pp. 89–95 in Colloque de topologie algébrique, Louvain, 1956 (Masson et Cie, Paris, 1957).Google Scholar