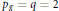Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chen, Jungkai
and
Hacon, Christopher
2006.
A surface of general type with pg= q = 2 and KX2= 5.
Pacific Journal of Mathematics,
Vol. 223,
Issue. 2,
p.
219.
Bauer, Ingrid C.
Catanese, Fabrizio
and
Pignatelli, Roberto
2006.
Global Aspects of Complex Geometry.
p.
1.
Penegini, Matteo
2011.
The classification of isotrivially fibred surfaces with p g = q = 2.
Collectanea mathematica,
Vol. 62,
Issue. 3,
p.
239.
Penegini, Matteo
and
Polizzi, Francesco
2013.
Surfaces with pg = q = 2, K2 = 6, and Albanese Map of Degree 2.
Canadian Journal of Mathematics,
Vol. 65,
Issue. 1,
p.
195.
Džambić, Amir
and
Roulleau, Xavier
2014.
Automorphisms and quotients of quaternionic fake quadrics.
Pacific Journal of Mathematics,
Vol. 267,
Issue. 1,
p.
91.
FRAPPORTI, DAVIDE
and
PIGNATELLI, ROBERTO
2015.
MIXED QUASI-ÉTALE QUOTIENTS WITH ARBITRARY SINGULARITIES.
Glasgow Mathematical Journal,
Vol. 57,
Issue. 1,
p.
143.
Bauer, Ingrid
Catanese, Fabrizio
and
Frapporti, Davide
2015.
Beauville Surfaces and Groups.
Vol. 123,
Issue. ,
p.
1.
Pignatelli, Roberto
2015.
Beauville Surfaces and Groups.
Vol. 123,
Issue. ,
p.
149.
Penegini, Matteo
and
Polizzi, Francesco
2017.
A note on surfaces with pg
= q = 2 and an irrational fibration.
Advances in Geometry,
Vol. 17,
Issue. 1,
p.
61.
Cancian, Nicola
and
Frapporti, Davide
2018.
On semi‐isogenous mixed surfaces.
Mathematische Nachrichten,
Vol. 291,
Issue. 2-3,
p.
264.
Penegini, Matteo
and
Pignatelli, Roberto
2022.
A note on a family of surfaces with $$p_g=q=2$$ and $$K^2=7$$.
Bollettino dell'Unione Matematica Italiana,
Vol. 15,
Issue. 1-2,
p.
305.
Alessandro, Massimiliano
and
Catanese, Fabrizio
2025.
Perspectives on Four Decades of Algebraic Geometry, Volume 1.
Vol. 351,
Issue. ,
p.
73.