We consider the Randers space $({{V}^{n}},\,{{F}_{b}})$ obtained by perturbing the Euclidean metric by a translation, 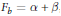${{F}_{b}}\,=\,\alpha \,+\,\beta $, where 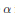$\alpha $ is the Euclidean metric and 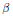$\beta $ is a 1-form with norm 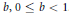$b,\,0\,\le \,b\,<\,1$. We introduce the concept of a hypersurface with constant mean curvature in the direction of a unitary normal vector field. We obtain the ordinary differential equation that characterizes the rotational surfaces 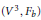$({{V}^{3}},\,{{F}_{b}})$ of constant mean curvature (cmc) in the direction of a unitary normal vector field. These equations reduce to the classical equation of the rotational cmc surfaces in Euclidean space, when 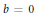$b\,=\,0$. It also reduces to the equation that characterizes the minimal rotational surfaces in 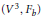$({{V}^{3}},\,{{F}_{b}})$ when 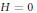$H\,=\,0$, obtained by M. Souza and K. Tenenblat. Although the differential equation depends on the choice of the normal direction, we show that both equations determine the same rotational surface, up to a reflection. We also show that the round cylinders are cmc surfaces in the direction of the unitary normal field. They are generated by the constant solution of the differential equation. By considering the equation as a nonlinear dynamical system, we provide a qualitative analysis, for 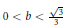$0\,<\,b\,<\,\frac{\sqrt{3}}{3}$. Using the concept of stability and considering the linearization around the single equilibrium point (the constant solution), we verify that the solutions are locally asymptotically stable spirals. This is proved by constructing a Lyapunov function for the dynamical systemand by determining the basin of stability of the equilibrium point. The surfaces of rotation generated by such solutions tend asymptotically to one end of the cylinder.