Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:50:13.217Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur Quelques Series de Lambert et de Dirichlet

Published online by Cambridge University Press:  20 November 2018

Jacques Touchard
Jacques Touchard*
Affiliation:
Lausanne, Suisse
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Nous nous occupons dans ce travail de séries dont voici le type le plus simple

et de leurs analogues lorsqu'on remplace xn par n-s et yn par n-s. Faute d'une autre désignation, nous avons cru pouvoir appeler ces séries respectivement séries de Lambert et séries de Dirichlet. Une série plus générale que la précédente est

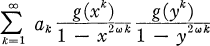
où les ak sont des constantes et où g(x) est un polynôme dont les coefficients sont des symboles de Jacobi (1, pp. 132-40; 4 pp 361-9).

possédant la période 2ω. Les expressions

ont des propriétés multiplicatives analogues à celles des sommes de Ramanujan (6) d'où l'on peut déduire deux propositions concernant les racines de g(x).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 12 , 1960 , pp. 1 - 19
Copyright
Copyright © Canadian Mathematical Society 1960

References

1. Bachmann, P., Zahlentheorie, Teil 1.Google Scholar
2. Bachmann, P. Zahlentheorie, Teil 2.Google Scholar
3. Brunel, G., Monographie de la fonction gamma.Google Scholar
4. Cahen, E., Théorie des nombres, T. 2.Google Scholar
5. Euler, L., Oeuvres, Series Prima Vol. X.Google Scholar
6. Hardy, G.H. and Wright, E.M., An introduction to the theory of numbers (2nd éd.; Oxford, 1954).Google Scholar
7. Landau, E., Primzahlen, vol. I.Google Scholar
8. Landau, E. Primzahlen, vol. II.Google Scholar
9. Lindelöf, E., Le Calcul des résidus.Google Scholar
10. Nielsen, N., Traité élémentaire des nombres de Bernoulli.Google Scholar
11. Schlömilch, O., Compendium der Höheren analysis, vol. II.Google Scholar