Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Herman, Richard H
and
Jones, Vaughan F.R
1982.
Period two automorphisms of UHF C∗-algebras.
Journal of Functional Analysis,
Vol. 45,
Issue. 2,
p.
169.
Robinson, P. L.
1993.
The even 𝐶* Clifford algebra.
Proceedings of the American Mathematical Society,
Vol. 118,
Issue. 3,
p.
713.
Power, S. C.
1997.
Operator Algebras and Applications.
p.
403.
Donsig, Allan P.
and
Power, S.C.
1997.
Homology for Operator Algebras.
Journal of Functional Analysis,
Vol. 150,
Issue. 1,
p.
240.
Power, S.C.
1999.
Relative Positions of Matroid Algebras.
Journal of Functional Analysis,
Vol. 165,
Issue. 2,
p.
205.
Izumi, Masaki
2004.
Finite group actions on C*-algebras with the Rohlin property, I.
Duke Mathematical Journal,
Vol. 122,
Issue. 2,
Baranov, A.A.
2013.
Classification of the direct limits of involution simple associative algebras and the corresponding dimension groups.
Journal of Algebra,
Vol. 381,
Issue. ,
p.
73.
Szabó, Gábor
2015.
A Short Note on the Continuous Rokhlin Property and the Universal Coefficient Theorem in E-theory.
Canadian Mathematical Bulletin,
Vol. 58,
Issue. 2,
p.
374.
Santiago, Luis
2015.
Crossed products by actions of finite groups with the Rokhlin property.
International Journal of Mathematics,
Vol. 26,
Issue. 07,
p.
1550042.
HØYNES, SIRI-MALÉN
2016.
Toeplitz flows and their ordered K-theory.
Ergodic Theory and Dynamical Systems,
Vol. 36,
Issue. 6,
p.
1892.
Gardella, Eusebio
and
Santiago, Luis
2016.
Equivariant ⁎-homomorphisms, Rokhlin constraints and equivariant UHF-absorption.
Journal of Functional Analysis,
Vol. 270,
Issue. 7,
p.
2543.


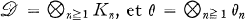 une symétrie de
une symétrie de 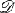 ; on associe à θ un entier généralisé
; on associe à θ un entier généralisé 