Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:49:11.315Z Has data issue: false hasContentIssue false
  • English
  • Français

Summability Methods on Matrix Spaces

Published online by Cambridge University Press:  20 November 2018

Josephine Mitchell
Josephine Mitchell*
Affiliation:
The Pennsylvania State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The matrix spaces under consideration are the four main types of irreducible bounded symmetric domains given by Cartan (5). Let z = (zjk) be a matrix of complex numbers, z' its transpose, z* its conjugate transpose and I = I(n) the identity matrix of order n. Then the first three types are defined by

(1)

where z is an n by m matrix (n ≤ m), a symmetric or a skew-symmetric matrix of order n (16). The fourth type is the set of complex spheres satisfying

(2)

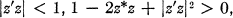
where z is an n by 1 matrix. It is known that each of these domains possesses a distinguished boundary B which in the first three cases is given by

(3)

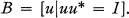
(In the case of skew symmetric matrices the distinguished boundary is given by (2) only if n is even.)

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 13 , 1961 , pp. 63 - 77
Copyright
Copyright © Canadian Mathematical Society 1961

References

1. Albert, A. A., Modern higher algebra (Chicago, 1937).Google Scholar
2. Bergman, S., The kernel function and conformai mapping, Math. Surveys, No. V (1950).Google Scholar
3. Bochner, S., Group invariance of Cauchy's formula in several variables, Ann. Math., 45 (1944), 686–707.Google Scholar
4. I'A Bromwich, T. J. and Hardy, G. H., Some extensions to multiple series of Abel's theorem on continuity, of power series, Proc. London Math. Soc, 2 (1905), 161–189.Google Scholar
5. Cartan, E., Sur les domains bornes homogènes de Vespace de n variables complexes, Abh. Math. Sem. Univ. Hamburg, 11 (1936), 116–162.Google Scholar
6. Hua, L. K., On the theory of functions of several complex variables, I-III, Acta Math. Sinica, 2 (1953), 288–323. 5 (1955), 1-25, 205-242; (in Chinese), M.R., 17 (1956), p. 191. Also Harmonic analysis of the classical domain in the study of analytic functions of several complex variables, mimeographed notes (about 1956).Google Scholar
7. Knopp, K., Limitierungs-Umkehrsdtze fur Doppelfolgen, Math. Z., 45 (1939), 573–589.Google Scholar
8. Lowdenslager, D. B., Potential theory and a generalized Jensen-Nevalinna formula for functions of several complex variables, Jn. Math. Mech., 7 (1958), 207–218.Google Scholar
9. Lowdenslager, D. B., Potential theory in bounded symmetric homogeneous complex domains, Ann. Math., 67 (1958), 467–484.Google Scholar
10. Macduffee, C. C., The theory of matrices (Ergebnisse der Mat. und ihrer Grenzgebiete [Chelsea, 1946]).Google Scholar
11. Mitchell, J., On double Sturm-Liouville series, Amer. J. Math., 65 (1943), 616–636.Google Scholar
12. Mitchell, J., An example of a complete orthonormal system and the kernel function in the geometry of matrices, Proceedings of the Second Canadian Mathematical Congress (Vancouver, 1949), 155–163.Google Scholar
13. Mitchell, J., On the spherical summability of multiple orthogonal series, Trans. Amer. Math. Soc, 71 (1951), 136–151.Google Scholar
14. Mitchell, J., Potential theory in the geometry of matrices, Trans. Amer. Math. Soc, 79 (1955), 401–422.Google Scholar
15. Mitchell, J., Orthogonal systems on matric spaces, West. Research Lab. Pub., Scientific Paper 60-94801-1-P2 (1956).Google Scholar
16. Morita, K., On the kernel functions of symmetric domains, Sci. Reports of Tokyo Kyoiku Daigaku Sec. A, 5 (1956), 190–212.Google Scholar
17. Titchmarsh, E. C., The theory of functions (2nd éd., Oxford University Press, 1939).Google Scholar
18. Tung, S. H., Tauberian theorems for multiple series, unpublished Master's thesis (The Pennsylvania State University).Google Scholar
19. Weyl, H., The classical groups (Princeton University Press, 1946).Google Scholar
20. Zygmund, A., Trigonometrical series, Monog. Mat., Tom V (Warsaw, 1935).Google Scholar
21. Hua, L. K. and Look, K. H., Theory of harmonic functions in classical domains, Sci. Sinicd, 8, No. 10 (1959), 1032–1094.Google Scholar