Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fillmore, P. A.
1973.
On invariant linear manifolds.
Proceedings of the American Mathematical Society,
Vol. 41,
Issue. 2,
p.
501.
Feintuch, Abie
and
Rosenthal, Peter
1973.
Remarks on reductive operator algebras.
Israel Journal of Mathematics,
Vol. 15,
Issue. 2,
p.
130.
Wiggen, Thomas P.
1974.
On direct sums of reductive operators.
Proceedings of the American Mathematical Society,
Vol. 45,
Issue. 2,
p.
313.
Radjavi, Heydar
and
Rosenthal, Peter
1974.
On transitive and reductive operator algebras.
Mathematische Annalen,
Vol. 209,
Issue. 1,
p.
43.
Shul'man, V. S.
1974.
Multiplication operators in C*-algebras and the problem of reflexivity of algebras which contain an m.a.s.a..
Functional Analysis and Its Applications,
Vol. 8,
Issue. 1,
p.
86.
Rosenthal, Peter
1975.
On reductive algebras containing compact operators.
Proceedings of the American Mathematical Society,
Vol. 47,
Issue. 2,
p.
338.
Nikol'skii, N. K.
1976.
Invariant subspaces in the theory of operators and theory of functions.
Journal of Soviet Mathematics,
Vol. 5,
Issue. 2,
p.
129.
Azoff, E. A.
Fong, C. K.
and
Gilfeather, F.
1976.
A reduction theory for non-self-adjoint operator algebras.
Transactions of the American Mathematical Society,
Vol. 224,
Issue. 2,
p.
351.
Naimark, M. A.
Loginov, A. I.
and
Shul'man, V. S.
1976.
Non-self-adjoint operator algebras in Hilbert space.
Journal of Soviet Mathematics,
Vol. 5,
Issue. 2,
p.
250.
Ansari, Mohamad A.
1985.
Reductive algebras containing a direct sum of the unilateral shift and a certain other operator are selfadjoint.
Proceedings of the American Mathematical Society,
Vol. 93,
Issue. 2,
p.
284.
Radjavi, Heydar
and
Rosenthal, Peter
2010.
A Glimpse at Hilbert Space Operators.
p.
341.
Cheng, Guozheng
Guo, Kunyu
and
Wang, Kai
2010.
Transitive algebras and reductive algebras on reproducing analytic Hilbert spaces.
Journal of Functional Analysis,
Vol. 258,
Issue. 12,
p.
4229.
Xu, An-jian
2019.
Reductivity and bundle shifts.
Applied Mathematics-A Journal of Chinese Universities,
Vol. 34,
Issue. 1,
p.
27.
Zou, Yang
2025.
Minimal Reducing Subspaces of 3-order Slant Toeplitz Operator on Hardy Space over the Disc.
Mathematics Letters,
Vol. 11,
Issue. 1,
p.
1.
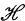 is
is 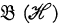
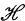 , operator algebra means weakly closed algebra of operators containing the identity, subspace means closed linear manifold, a non-trivial subspace is a subspace other than {0} and
, operator algebra means weakly closed algebra of operators containing the identity, subspace means closed linear manifold, a non-trivial subspace is a subspace other than {0} and 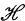 , a. hyperinvariant subspace for A is a subspace invariant under every operator which commutes with A, a transitive operator algebra is one without any non-trivial invariant subspaces and
, a. hyperinvariant subspace for A is a subspace invariant under every operator which commutes with A, a transitive operator algebra is one without any non-trivial invariant subspaces and 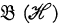 denotes the algebra of all operators on
denotes the algebra of all operators on 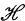 .
.